MATH 1830

1.1 Finding Limits Graphically

Pre-Class:

• Take notes on the videos and readings (use the space below).
• Work and check problems #1-7 in the 1.1 NOTES section.
• Complete the 1.1 Pre-Class Quiz.

Introduction

1. Box Office Receipts

   The total worldwide box-office receipts for a long running indie film are approximated by the function $$T(x) = \frac{{120{x^2}}}{{{x^2} + 4}}$$ where T(x) is measured in millions of dollars and x is the number of months since the movie’s release. What are the total box-office receipts after:

   1. The first month?

      $T\left( 1 \right) = \frac{{120{{\left( 1 \right)}^2}}}{{{1^2} + 4}} = 24$ The total box-office receipts after 1 month are \$24 million.

   2. The second month?

      $T\left( 2 \right) = \frac{{120{{\left( 2 \right)}^2}}}{{{2^2} + 4}} = 60$ The total box-office receipts after 2 months are \$60 million.

   3. The third month?

      $T\left( 3 \right) = \frac{{120{{\left( 3 \right)}^2}}}{{{3^2} + 4}} = 83$ The total box-office receipts after 3 months are \$83 million.

   4. The hundredth month?

      $T\left( {100} \right) = \frac{{120{{\left( {100} \right)}^2}}}{{{{100}^2} + 4}} = 119.95$ The total box-office receipts after 100 months are \$119.95 million.

   5. What will the movie gross in the long run? (When x is very large.)

      In the long run, the movie will gross approximately \$120 million.

2. Driving Costs

   A study of driving costs of 1992 model subcompact cars found that the average cost (car payments, gas, insurance, upkeep, and depreciation), measured in cents/mile, is approximated by $$C(x) = \frac{{2010}}{{{x^{2.2}}}} + 17.80$$ where x denotes the number of miles (in thousands of miles) the car is driven in a year. What is the average cost of driving a subcompact car:

   1. 5,000 miles per year?

      $C\left( 5 \right) = \frac{{2010}}{{{5^{2.2}}}} + 17.80 = 76.10$

      The average cost when driving 5,000 miles per year is 76.1 cents per mile.

   2. 10,000 miles per year?

      $C\left( {10} \right) = \frac{{2010}}{{{{10}^{2.2}}}} + 17.80 = 30.50$

      The average cost when driving 10,000 miles per year is 30.5 cents per mile.

   3. 25,000 miles per year?

      $C\left( {25} \right) = \frac{{2010}}{{{{25}^{2.2}}}} + 17.80 = 19.50$

      The average cost when driving 25,000 miles per year is 19.5 cents per mile.

   4. 50,000 miles per year?

      $C\left( {50} \right) = \frac{{2010}}{{{{50}^{2.2}}}} + 17.80 = 18.17$

      The average cost when driving 50,000 miles per year is 18.2 cents per mile.

   5. What happens to the average cost as the number of miles driven increases without bound?

      The average cost approaches 17.8 cents per mile when the car is driven “infinite” miles in a year.

   6. Verify by evaluating the cost when the number of miles is 1,000,000 (or any large number).

      $C\left( {1000} \right) = \frac{{2010}}{{{{1000}^{2.2}}}} + 17.80$

      The average cost per mile is approximately 17.80 cents per mile when the car is driven 1,000,000 miles per year.

   Source https://domoremath.files.wordpress.com/2013/09/limits-word-prob-with-solns.pdf

Notes

Limits: A Graphical Approach

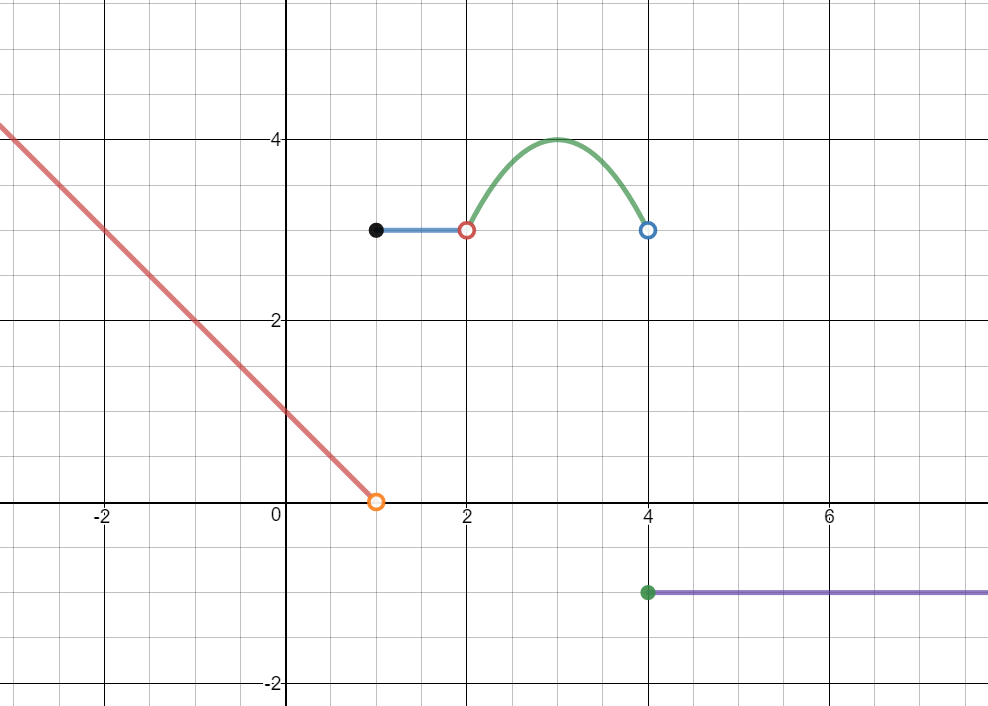
$f(x)= \begin{cases} -x+1 & x \lt 1 \\ 3 & 1\leq x\lt 2 \\ -\left(x-3\right)^2+4 & 2 \lt x \lt 4\\ -1 & x\geq 4\\ \end{cases} $

Use the piecewise function to answer the questions below.

Evaluate the limits graphically. If the limit does not exist, explain why.

1. $\mathop {\lim }\limits_{x\; \to {0^ - }} f\left( x \right) =$ $1$

2. $\mathop {\lim }\limits_{x\; \to {0^ + }} f\left( x \right) =$ $1$

3. $\mathop {\lim }\limits_{x\; \to 0} f\left( x \right) =$ $1$

4. $f\left( 0 \right) = $ $1$

5. $\mathop {\lim }\limits_{x\; \to {1^ - }} f\left( x \right) =$ $0$

6. $\mathop {\lim }\limits_{x\; \to {1^ + }} f\left( x \right) =$ $3$

7. $\mathop {\lim }\limits_{x\; \to 1} f\left( x \right)=$ Does not exist

   The limits from the left and right are not equal, so the limit does not exist.

8. $f\left( 1 \right) =$ $3$

9. $\mathop {\lim }\limits_{x\; \to {2^ - }} f\left( x \right) =$ $3$

10. $\mathop {\lim }\limits_{x\; \to {2^ + }} f\left( x \right) =$ $3$

11. $\mathop {\lim }\limits_{x\; \to 2} f\left( x \right) =$ $3$

12. $f\left( 2 \right) =$ undefined

13. Is it possible to define $f\left( 1 \right)$ so that $\mathop {\lim }\limits_{x\; \to 1} f\left( x \right) = f\left( 1 \right)$? Explain.

    No. The limit does not exist. There is a jump in the graph.

14. Is it possible to redefine $f\left( 2 \right)$ so that $\mathop {\lim }\limits_{x\; \to 2} f\left( x \right) = f\left( 2 \right)$? Explain.

    Yes. Let $f\left( 2 \right) = \;3$

15. $\mathop {\lim }\limits_{x\; \to - 1} f\left( x \right) =$ $2$

16. $\mathop {\lim }\limits_{x\; \to 4} f\left( x \right) =$ Does not exist

    The limits from the left and right are not equal, so the limit does not exist.

17. $\mathop {\lim }\limits_{x\; \to 6} f\left( x \right) =$ $-1$

18. $\mathop {\lim }\limits_{x\; \to 3} f\left( x \right) =$ $4$

19. $\mathop {\lim }\limits_{x\; \to - 2} f\left( x \right) =$ $3$