1.4 Definition of the Derivative
Pre-Class:
- Complete 1.3 Homework assignment: check and correct.
- Take notes on the videos and readings (use the space below).
- Work and check problem #1 in the 1.4 NOTES section.
- Complete the 1.4 Pre-Class Quiz.
Introduction
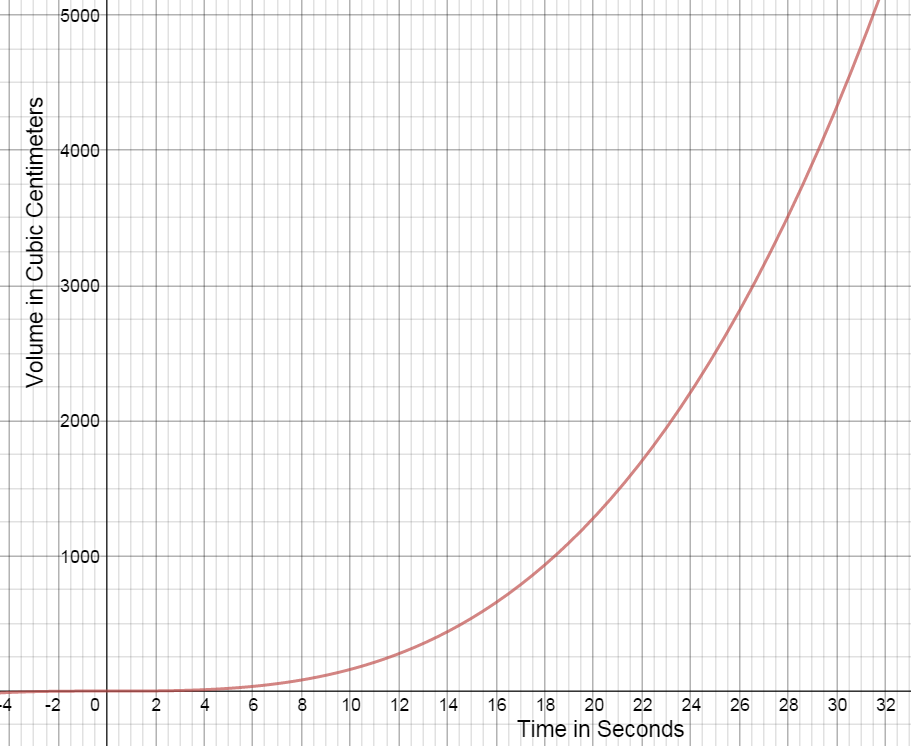
A decorative birthday balloon is being filled with helium. The table shows the volume of the helium in the balloon at 3 second intervals for 30 seconds.
| t(seconds) | V (cubic centimeters) |
|---|---|
| 0 | 0 |
| 3 | 4.2 |
| 6 | 33.5 |
| 9 | 113.0 |
| 12 | 267.9 |
| 15 | 523.3 |
| 18 | 904.3 |
| 21 | 1436.0 |
| 24 | 2143.6 |
| 27 | 3052.1 |
| 30 | 4186.7 |
This function can be approximated by the equation $f(x) = 0.16{x^3} + 0.0003{x^2} - 0.007x + 0.0161$ (graphed below).
-
What are the dependent and independent variables for this problem? In what units is the rate of changed expressed?
The dependent variable is volume, in $cm^3.$
The independent variable is time, in seconds.
The rate of change is measured in $cm^3$ per second $({}^{c{{m}^{3}}}/{}_{\sec }).$
-
A secant line is a line that intersects two points on a curve. Draw a secant line on the graph for each of the following. Calculate the slope of the secant line for each of the following intervals.
- 21 s to 30 s
$\left(21,1436\right)\;\left(30,4186.7\right)\;\;{m_{secant}}\approx306\;cm^3/sec$
- 21 s to 27 s
$\left(21,1436\right)\;\left(27,3052.1\right)\;\;{m_{secant}}\approx269\;cm^3/sec$
- 21 s to 24 s
$\left(21,1436\right)\;\left(24,2143.6\right)\;\;{m_{secant}}\approx236\;cm^3/sec$
- 21 s to 30 s
-
What does the slope of the secant line represent?
The slope of the secant represents the average rate of change in the volume of helium in the balloon over the time interval.
-
A tangent line is a line that intersects a curve at only one point. Draw a tangent line at the point on the graph corresponding to 21 s and estimate the slope of this line.
Answers will vary. At 21 seconds, the volume of the helium balloon is increasing at a rate of approximately $208 \;cm^3/sec.$
-
What does the slope of the tangent line represent?
The slope of the tangent line represents the instantaneous rate of change of the volume at a given time. At 21 seconds, the volume of the helium balloon is increasing at a rate of approximately $208 \;cm^3/sec.$
-
Compare the secant slopes to the slope of the tangent line. What do you notice?
As the time interval becomes smaller between 21 sec and the end of the interval, the slope of the secant line gets closer in value to the slope of the tangent line, which is the rate of change at exactly 21 seconds.
Source http://mysite.science.uottawa.ca/iabde083/ch01.pdf
Notes
Limit Definition of the Derivative of a Function: 4 Step ProcessGiven $f(x)$,
$f'(x)=\mathop {\lim }\limits_{h \to 0} \frac{{f\left( {x + h} \right) - f\left( x \right)}}{h}$
Step 1: Find $f\left( {x + h} \right)$
Step 2: Find $f\left( {x + h} \right) - f\left( x \right)$
Step 3: Find $\frac{{f\left( {x + h} \right) - f\left( x \right)}}{h}$
Step 4: Find $\mathop {\lim }\limits_{h \to 0} \frac{{f\left( {x + h} \right) - f\left( x \right)}}{h}$
-
Use the limit definition of the derivative to find $f'\left( x \right)$, given $f\left( x \right) = \;{x^2}\; - 3x - 2.$
Step 1
$f(x + h) = {(x + h)^2} - 3(x + h) - 2$
$f(x + h) = {x^2} + 2xh + {h^2} - 3x - 3h - 2$
Step 2
$f(x + h) - f(x) = \left( {{x^2} + 2xh + {h^2} - 3x - 3h - 2} \right) - \left( {{x^2}\; - 3x - 2} \right)$
$f(x+h)-f(x)= 2xh + {h^2} - 3h$
Step 3
$\frac{{f(x + h) - f(x)}}{h} = \frac{{2xh + {h^2} - 3h}}{h}$
$ \frac{{f(x + h) - f(x)}}{h} = \frac{{2xh}}{h} + \frac{{{h^2}}}{h} - \frac{{3h}}{h}$
$\frac{{f(x + h) - f(x)}}{h} = 2x + h - 3$
Step 4
$\mathop {\lim }\limits_{h \to 0} 2x + h - 3 = 2x + (0) - 3 = 2x - 3$
Therefore, the slope of the tangent line for any given $x$ is $f'(x) = 2x - 3.$
-
Use the limit definition of the derivative to find $f'\left( x \right)$, given $f\left( x \right) = \;5{x^2} + 2x - 8.$
Step 1
$f(x + h) = 5{(x + h)^2} + 2(x + h) - 8$
$f(x+h)= 5({x^2} + 2xh + {h^2}) + 2x + 2h - 8$
$f(x+h)=5{x^2} + 10xh + 5{h^2} + 2x + 2h - 8$
Step 2
$f(x + h) - f(x) = \left( {5{x^2} + 10xh + 5{h^2} + 2x + 2h - 8} \right) - \left( {5{x^2} + 2x - 8} \right)$
$f(x+h)-f(x)= 10xh + 5{h^2} + 2h$
Step 3
$\frac{{f(x + h) - f(x)}}{h} = \frac{{10xh + 5{h^2} + 2h}}{h}$
$ \frac{{f(x + h) - f(x)}}{h} = \frac{{10xh}}{h} + \frac{{5{h^2}}}{h} + \frac{{2h}}{h}$
$\frac{{f(x + h) - f(x)}}{h} = 10x + 5h + 2$
Step 4
$\mathop {\lim }\limits_{h \to 0} (10x + 5h + 2) = 10x + 5(0) + 2 = 10x + 2$
Therefore, the slope of the tangent line for any given $x$ is $f'(x) = 10x + 2.$
Write the equation of the tangent line at x=2.Point $\quad f(2)=16\quad \quad (2,16)$
Slope $\quad {m_{tan}} = f'(2) = 10(2) + 2 = 20 + 2 = 22$
$y-y_1=m\left(x-x_1\right)\\ $
$y - 16 = 22(x - 2)$
$y - 16 = 22x - 44$
$y = 22x - 28$
-
Use the limit definition of the derivative to find $f'\left( x \right)$, given $f(x) = - 4{x^2} + x + 2.$
Step 1
$f(x+h)=-4{{(x+h)}^{2}}+(x+h)+2$
$f(x+h)=-4({{x}^{2}}+2xh+{{h}^{2}})+x+h+2$
$f(x+h)=-4{{x}^{2}}-8xh-4{{h}^{2}}+x+h+2$
Step 2
$f(x+h)-f(x)=\left( -4{{x}^{2}}-8xh-4{{h}^{2}}+x+h+2 \right)-\left( -4{{x}^{2}}+x+2 \right)$
$f(x+h)-f(x)=-8xh-4{{h}^{2}}+h$
Step 3
$\frac{f(x+h)-f(x)}{h}=\frac{-8xh-4{{h}^{2}}+h}{h}$
$\frac{f(x+h)-f(x)}{h}=\frac{-8xh}{h}-\frac{4{{h}^{2}}}{h}+\frac{h}{h}$
$\frac{f(x+h)-f(x)}{h}=-8x-4h+1$
Step 4
$\mathop {\lim }\limits_{h \to 0} (-8x-4h+1)=-8x-4(0)+1=-8x+1$
Therefore, the slope of the tangent line for any given $x$ is ${f}'(x)=-8x+1.$
Write the equation of the tangent line at x = 1.
Point $\quad f(1)=-1\quad \quad (1, - 1)$
Slope $\quad {m_{\tan}}= f'(1) =- 8(1) + 1 = - 8 + 1 = - 7$
$y-y_1=m\left(x-x_1\right)\\ $
$y +1 = -7(x - 1)$
$y +1 = -7x +7$
$y = -7x +6$
-
Use the limit definition of the derivative to find $f'\left( x \right)$, given $f\left( x \right) = \;\frac{6}{x} - 2.$
Step 1
$f(x + h) = \frac{6}{{x + h}} - 2$
Step 2
$f(x + h) - f(x) = \frac{6}{{x + h}} - \frac{6}{x}$
$f(x + h) - f(x) = \frac6{x+h}\left(\frac xx\right)-\frac6x\left(\frac{x+h}{x+h}\right)$
$f(x + h) - f(x) = \frac{{6x}}{{x(x + h)}} - \frac{{6x + 6h}}{{x(x + h)}}$
$f(x + h) - f(x) = \frac{{ - 6h}}{{x(x + h)}}$
Step 3
$\frac{{f(x + h) - f(x)}}{h} = \frac{{\left( {\frac{{ - 6h}}{{x(x + h)}}} \right)}}{h}$
$\frac{{f(x + h) - f(x)}}{h} = \frac{-6h}{x(x+h)}\cdot\frac1h = \frac{{ - 6}}{{x(x + h)}}$
Step 4
$\mathop {\lim }\limits_{h \to 0} \frac{{ - 6}}{{x(x + h)}} = \frac{{ - 6}}{{x(x + 0)}} = \frac{{ - 6}}{{x(x)}} = \frac{{ - 6}}{{{x^2}}}$
Therefore, the slope of the tangent line for any given $x$ is $f'\left( x \right) = -\frac{{ 6}}{{{x^2}}}.$
Find the equation of the tangent line at $x = 3.$Point $\quad f(3)=0\quad (3,0)$
Slope $\quad {m_{\tan}} = f'(3) = \frac{{ - 6}}{9} = - \frac{2}{3}$
$y-y_1=m\left(x-x_1\right)\\ $
$y -0 = - \frac{2}{3}(x - 3)$
$y = - \frac{2}{3}x + 2$
-
Friedman Academy is a charter school in South Texas. The school is not at capacity, and enrollment increases monthly. The charter school’s enrollment is modeled by $$f\left( x \right) = {x^2}\; + x + 100$$ where y is in students and x is in years since 2008.
- Estimate the average change in enrollment (the average rate of change of y with respect to x) from the year
2010 to the year 2012.
Use points $(2,106)$ and $(4,120)$
Avg change: $\frac{120-106}{4-2}=\frac{14}{2}=7$
Enrollment increases by 7 students per year.
- Find the function for the instantaneous rate of change in enrollment using the limit definition of the derivative.
Step 1
$f(x + h) = {(x + h)^2} + (x + h) + 100=$
${x^2} + 2xh + {h^2} + x + h + 100$
Step 2
$f(x + h) - f(x) =( {{x^2} + 2xh + {h^2} + x + h + 100}) - ({{x^2} + x + 100})$
$f(x + h) - f(x)= 2xh + {h^2} + h$
Step 3
$\frac{{f(x + h) - f(x)}}{h} = \frac{{2xh + {h^2} + h}}{h}$
$\frac{{f(x + h) - f(x)}}{h} = \frac{{2xh}}{h} + \frac{{{h^2}}}{h} + \frac{h}{h}$
$\frac{{f(x + h) - f(x)}}{h} = 2x + h + 1$
Step 4
$\mathop {\lim }\limits_{h \to 0}\,\left( 2x+h+1 \right)=2x+(0)+1=2x+1$
Therefore, the function for the instanteous rate of change for any year is${f}'(x)=2x+1.$
- Use the equation to calculate the instantaneous change in enrollment in 2010, 2011, and 2012.
$f'(2) = 2(2) + 1 = 4 + 1 = 5$ In 2010, enrollment is increasing by 5 students per year.
$f'(3) = 2(3) + 1 = 6 + 1 = 7$ In 2011, enrollment is increasing by 7 students per year.
$f'(4) = 2(4) + 1 = 8 + 1 = 9$ In 2012, enrollment is increasing by 9 students per year.
- Estimate the average change in enrollment (the average rate of change of y with respect to x) from the year
2010 to the year 2012.
-
Suppose an object moves along the y axis so that its location is $f\left( x \right)=2{{x}^{2}}~+3x$ at time x. $f(x)$ is in meters and x is in seconds.
- Find the average velocity (the average rate of change of y with respect to x) for x changing from 2 to 4
sec.
Use the points $(2,14)$ and $(4,44)$
$avg\ rate\ of\ change=\frac{44-14}{4-2}=\frac{30}{2}=$
The average velocity from 2 to 4 seconds is $15m/s.$
- Use the limit definition of the derivative to find the instantaneous velocity.
Step 1
$f(x + h) = 2{(x + h)^2} + 3(x + h)$
$f(x + h)= 2({x^2} + 2xh + {h^2}) + 3x + 3h$
$f(x + h)= 2{x^2} + 4xh + 2{h^2} + 3x + 3h$
Step 2
$f(x + h) - f(x) = \left( {2{x^2} + 4xh + 2{h^2} + 3x + 3h} \right) - \left( {2{x^2} + 3x} \right)$
$f(x + h) - f(x)= 4xh + 2{h^2} + 3h$
Step 3
$\frac{{f(x + h) - f(x)}}{h} = \frac{{4xh + 2{h^2} + 3h}}{h}$
$\frac{{f(x + h) - f(x)}}{h} = \frac{{4xh}}{h} + \frac{{2{h^2}}}{h} + \frac{{3h}}{h}$
$\frac{{f(x + h) - f(x)}}{h} = 4x + 2h + 3$
Step 4
$\mathop {\lim }\limits_{h \to 0} \left( {4x + 2h + 3} \right) = 4x + 2\left( 0 \right) + 3 = 4x + 3$
Therefore, the instantaneous velocity at a given $x$ is $f'(x) = 4x + 3.$
- The instantaneous velocity at x = 2 seconds, 3 seconds, and 4 seconds.
$f'(2) = 4(2) + 3 = 8 + 3 = 11 $ The instantaneous velocity at 2 seconds is $11\;m/s.$
$f'(3) = 4(3) + 3 = 12 + 3 = 15 $ The instantaneous velocity at 3 seconds is $15\;m/s.$
$f'(4) = 4(4) + 3 = 16 + 3 = 19 $ The instantaneous velocity at 4 seconds is $19\;m/s.$
- Find the average velocity (the average rate of change of y with respect to x) for x changing from 2 to 4
sec.