MATH 1830

1.6 Marginal Analysis in Business and Economics

Pre-Class:

• Complete 1.5B Homework assignment: check and correct.
• Take notes on the videos and readings (use the space below).
• Work and check problems #1-7, 11-16 in the 1.6 INTRO section.
• Complete the 1.6 Pre-Class Quiz.

Introduction

The cost, in dollars, of producing $x$ frozen fruit yogurt bars per day can be modeled by the function $$C(x) = 3450 + 1.5x - 0.0001{x^2}\quad when\quad 0 \le \,\,x\, \le 5000.$$

The revenue from selling $x$ yogurt bars is

Cost, Revenue, & Profit

1. What does 3450 represent in the cost function?

   3450 is the initial cost (machine, etc) and any static daily costs. This is the cost to the company even if zero bars are produced.

2. What does 3.25 represent in the revenue function?

   A good assumption would be the bars are selling at \$3.25 each.

3. What is the cost of producing 0 yogurt bars? What is the revenue generated from selling this many bars? What is the profit for selling 0 bars?

   $C\left( 0 \right) = 3450$

   The cost for producing 0 bars is \$3450, the initial cost.

   $R\left( 0 \right) = 0$

   When 0 bars are produced, the revenue is $0.

   $P\left( x \right) = R\left( x \right) - C\left( x \right)$

   $P\left( 0 \right) = 0 - 3450 = - 3450$

   Profit is -\$3450 if no yogurt bars are made and sold.

4. What is the cost of producing 1000 yogurt bars? What is the revenue generated from selling this many bars? What is the profit for selling 1000 bars?

   $C\left( {1000} \right) = 4850$

   The cost for producing 1000 bars is $4850.

   $R\left( {1000} \right) = 3250$

   The revenue for producing and selling 1000 bars is $3250.

   $P\left( {1000} \right) = 3250 - 4850 = - 1600$

   If 1000 yogurt bars are made and sold, the profit loss is - \$1600.

5. What is the cost of producing 5000 yogurt bars? What is the revenue generated from selling this many bars? What is the profit for selling 5000 bars?

   $C\left( {5000} \right) = 8450$

   The cost for producing 5000 bars is $8450.

   $R\left( {5000} \right) = 16250$

   The revenue for producing and selling 5000 bars is $16,250.

   $P\left( {5000} \right) = 16250 - 8450 = 7800$

   Profit is $7800 if 5000 yogurt bars are made and sold.

6. Find the model for the profit function, $P\left( x \right)$.

   $P\left( x \right) = R\left( x \right) - C\left( x \right) = \left( {3.25x} \right) - \left( {3450 + 1.5x - 0.0001{x^2}} \right)$

   $P(x)= 0.0001{x^2} + 1.75x - 3450$

   

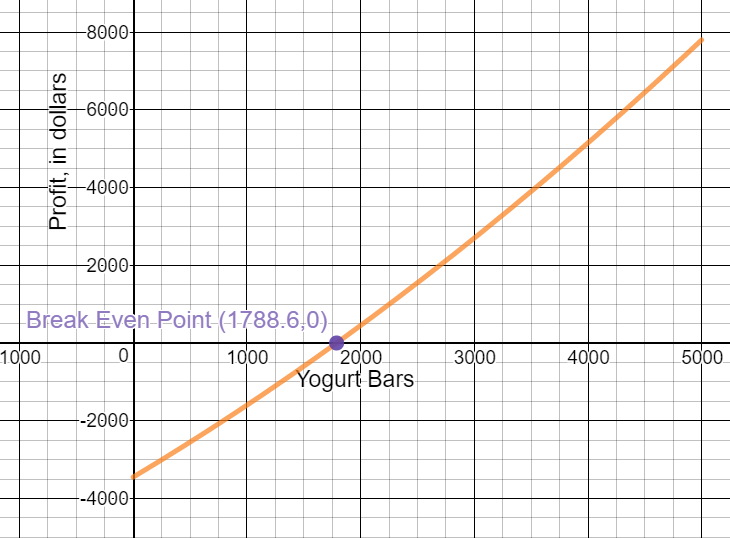
7. Answer the following questions about the model:

   When is the profit function positive?

   When production is greater than 1788.6 yogurt bars. For our example, when production is greater than or equal to 1788 yogurt bars.

   When is it negative?

   When production is less than 1788.6 yogurt bars. For our example, when production is less than 1789 yogurt bars.

   What important information does this provide the business owner?

   The owner needs to produce and sell at least 1789 bars to break even and/or to make a profit.

   Average Cost, Revenue, & Profit

8. It is clear from 3, 4, & 5 that the cost, revenue, and profit change based on the number of yogurt bars produced/sold. How would you determine the AVERAGE cost, revenue, and profit?

   Use the following equations that were identified earlier in this introduction:

   $C(x) = 3450 + 1.5x - 0.0001{x^2}\quad when\quad 0 \le \,\,x\, \le 5000$

   $R(x) = 3.25x$

   $P(x) = 0.0001{x^2} + 1.75x - 3450$

   1. $\bar C\left( x \right)\, = \frac{{C\left( x \right)}}{x} = \frac{{3450 + 1.5x - 0.0001{x^2}}}{x}=$

      $\bar C(x)=\frac{{3450}}{x} + 1.5 - 0.0001x$

   2. $\bar R\left( x \right)\, = \frac{{R\left( x \right)}}{x} = \frac{{3.25x}}{x} = $

      $\bar R=3.25$

   3. $\bar P\left( x \right)\, = \frac{{P\left( x \right)}}{x} = \frac{{0.0001{x^2} + 1.75x - 3450}}{x} =$

      $\bar P= 0.0001x + 1.75 - \frac{{3450}}{x}$

9. Find the average cost and explain the result:

   1. $\bar C(0)\, =$

      undefined (Can't divide by zero.)

   2. $\bar C(1000)\, =$

      $4.85$

      At a production level of 1000 bars, the average cost to produce one bar is $4.85.

   3. $\bar C(5000)\,$ =

      $1.69$

      At a production level of 5000 bars, the average cost to produce one bar is $1.69.

10. Is there a difference in the average cost when the number of bars produced changes? Why or why not?

    Yes. Average cost decreases as the production level increases. The initial costs are divided by a larger number thus decreasing the amount per bar.

    Marginal Cost, Revenue, & Profit

    Use these equations generated earlier:

    $C(x) = 3450 + 1.5x - 0.0001{x^2}\quad when\quad 0 \le \,\,x\, \le 5000$

    $R(x) = 3.25x$

    $P(x) = 0.0001{x^2} + 1.75x - 3450$

11. Determine $C'\left( x \right)$. What does this represent?

    $C'\left( x \right) = 1.5 - 0.0002x$

    $C'\left( x \right)$ represents the estimated cost to produce one more bar, at a production level of x bars.

12. Determine $C'\left( {1000} \right)$. Interpret this result.

    $C'\left( {1000} \right) = 1.5 - 0.0002\left( {1000} \right) = 1.3$

    At a production rate of 1000 bars, the cost to produce the 1001th bar is estimated to be $1.30.

13. When is $C'\left( x \right) = 0$? Explain your answer.

    $1.5 - 0.0002x = 0$

    $1.5 = 0.0002x$

    $7500 = x$

    Within our domain, $C'\left( x \right)$ will never equal 0. 7500 yogurt bars is outside the domain of the function.

14. Determine $R'\left( x \right)$. What does this represent?

    $R'\left( x \right) = 3.25$

    $R'\left( x \right)$ represents the estimated revenue to produce one more bar, at a production level of x bars.

    $R'\left( x \right)$ is a constant function, therefore the revenue for one more bar will be \$3.25 at any level of production. We assumed earlier they were sold at a fixed price of \$3.25 each.

15. Determine $P'\left( x \right)$. What does this represent?

    $P'\left( x \right) = 0.0002x + 1.75$

    $P'\left( x \right)$ represents the estimated profit that will be earned if the company produces one more bar, at a production level of x bars.

16. How do marginal cost, revenue, & profit relate to our discussions about average rate of change and instantaneous rate of change?

    These marginal functions calculate the instantaneous rate of change at any production level.

Notes

Cost and Marginal Cost

Marginal Cost, Revenue and Profit

1. A company’s market research department recommends the manufacture and marketing of a new 3 meter lightening-to-USB power cord. After suitable test marketing, the research department presents the following price demand equation: $$p = 12 - 0.001x$$ where x is demand at price p. The financial department provides the cost function that includes a fixed cost of \$5600 (tooling and overhead) and variable costs of \$1.80 per power cord (materials, labor, marketing, transportation, storage): $$C\left( x \right) = 5600 + 1.80x$$

   1. Marginal Cost Function: Find and interpret the Marginal Cost Function

      $C'(x) = 1.80$

      At any production level, the cost to produce one more power cord is \$1.80.

   2. Revenue Function: Find the Revenue Function as a function of x.

      Revenue is price multiplied by production level

      $R(x) = px = \left( {12 - 0.001x} \right)x$

      $R(x)=12x - 0.001{x^2}$

   3. Marginal Revenue Function: Find the Marginal Revenue function and find the marginal revenue at x = 2000, x = 5000, and x = 7000. Interpret the results.

      $R'\left( x \right) = 12 - 0.002x$

      $R'\left( {2000} \right) = 12 - 0.002\left( {2000} \right) = 8$

      Revenue increases by \$8 for the 2001st cord produced and sold.

      $R'\left( {5000} \right) = 2$

      Revenue increases by \$2 for the 5001st cord produced and sold.

      $R'\left( {7000} \right) = - 2$

      Revenue decreases by \$2 for the 7001st cord produced and sold.

   4. Cost and Revenue Functions: Graph the cost function and the revenue function in the same coordinate system. Find the intersection points of these two graphs and interpret the results.

      

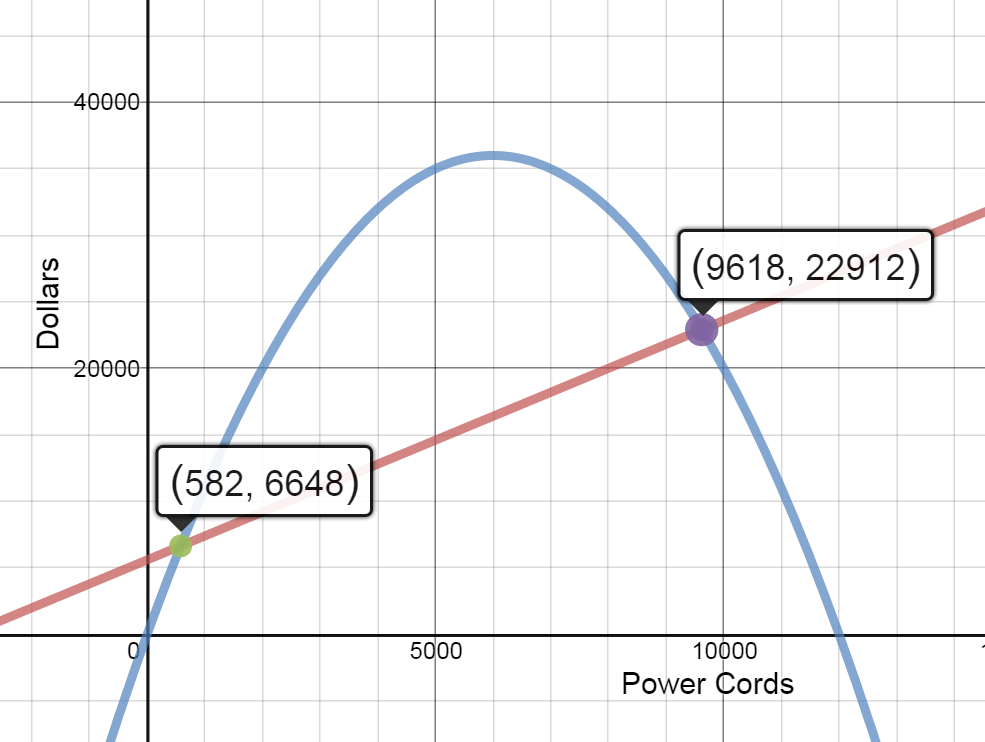
      At any production level between 0 and 582 power cords, revenue is less than cost. Therefore profit is negative.

      At any production level between 582 and 9618 power cords, revenue is greater than cost. Therefore profit is positive.

      At any production level great than 9618 power cords, revenue is less than cost. Therefore profit is negative.

   5. Profit Function: Find the profit function. Sketch the graph.

      

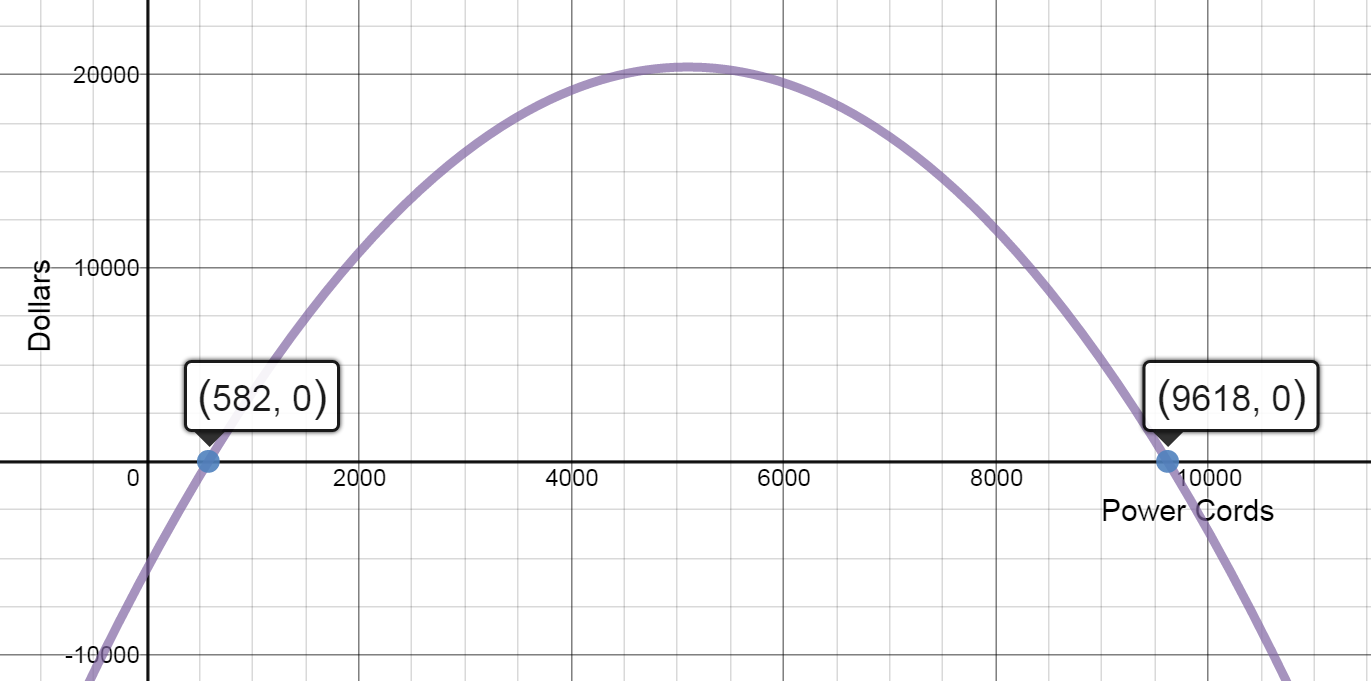
      $P(x) = R(x) - C(x) = (12x - 0.001{x^2}) - (5600 + 1.8x) = $

      $P(x)=- 0.001{x^2} + 10.2x - 5600$

   6. Marginal Profit Function: Find the marginal profit function and evaluate the marginal profit at x = 1000, x = 4000, and x = 6000. Interpret the results.

      $P'\left( x \right) = - 0.002x + 10.2$

      $P'(1000) = - 0.002(1000) + 10.2 = 8.2$

      Profit increases by \$8.20 for the 1001st cord.

      $P'(4000) = - 0.002(4000) + 10.2 = 2.2$

      Profit increases by \$2.20 for 4001st cord.

      $P'(6000) = - 0.002(6000) + 10.2 = - 1.8$

      Profit decreases by \$1.80 for 6001st cord.

   Marginal and Average Cost, Revenue, and Profit:

2. A shop manufactures performance bikes. The manager estimates that the total cost (in dollars) of producing b bikes is: $$C\left( b \right) = 1200 + 25b - 0.14{b^2}$$

   1. Average Cost: Find the average cost function, $\bar C\left( b \right)$. Calculate $\bar C\left( 7 \right)$ and interpret the results.

      $\bar C\left( b \right)\, = \frac{{1200 + 25b - 0.14{b^2}}}{b}$

      $\bar C\left( b \right)\, = \frac{{1200}}{b} + 25 - 0.14b$

      $\bar C\left( 7 \right)\, = \frac{{1200}}{7} + 25 - 0.14(7) = 195.45$

      The average cost of producing 7 bikes is \$195.45.

   2. Marginal Cost: Find the Marginal Cost Function,$ C'\left( b \right)$. Calculate $ {C'} \left( 7 \right)$ and interpret the results.

      $ C\left( b \right)\, = 1200 + 25b - 0.14{b^2}$

      ${C ^\prime }\left( b \right) = 25-0.28b$

      ${ C ^\prime }\left( 7 \right) = 23.04$

      When the 8th bike is produced, the average cost per bike decreases by \$24.63.

   3. Explain the difference between parts a and b.

      On average, the cost to produce each of the 7 bikes is \$195.45. The cost to produce the 8th bike is approximately \$23.04.