MATH 1830

Unit 4: Integration

4.1 Area by Sums

Pre-Class:

Print

Read

Watch

4.1 Quiz

Resources

Introduction

  1. The rate of change of the population (in thousands of people per year) of North Dakota between 1985 and 1996 can be modeled by

    $p(t)= \begin{cases} -7.35 & 0\leq t\leq 6 \\ 2.5 & 6 \lt t \leq 11\\ \end{cases} $ where t represents the number of years since 1985.

    (Source: Statistical Abstract, 1998)

    1. Sketch a graph of the rate of change function.

      Blank Cartesian Plane

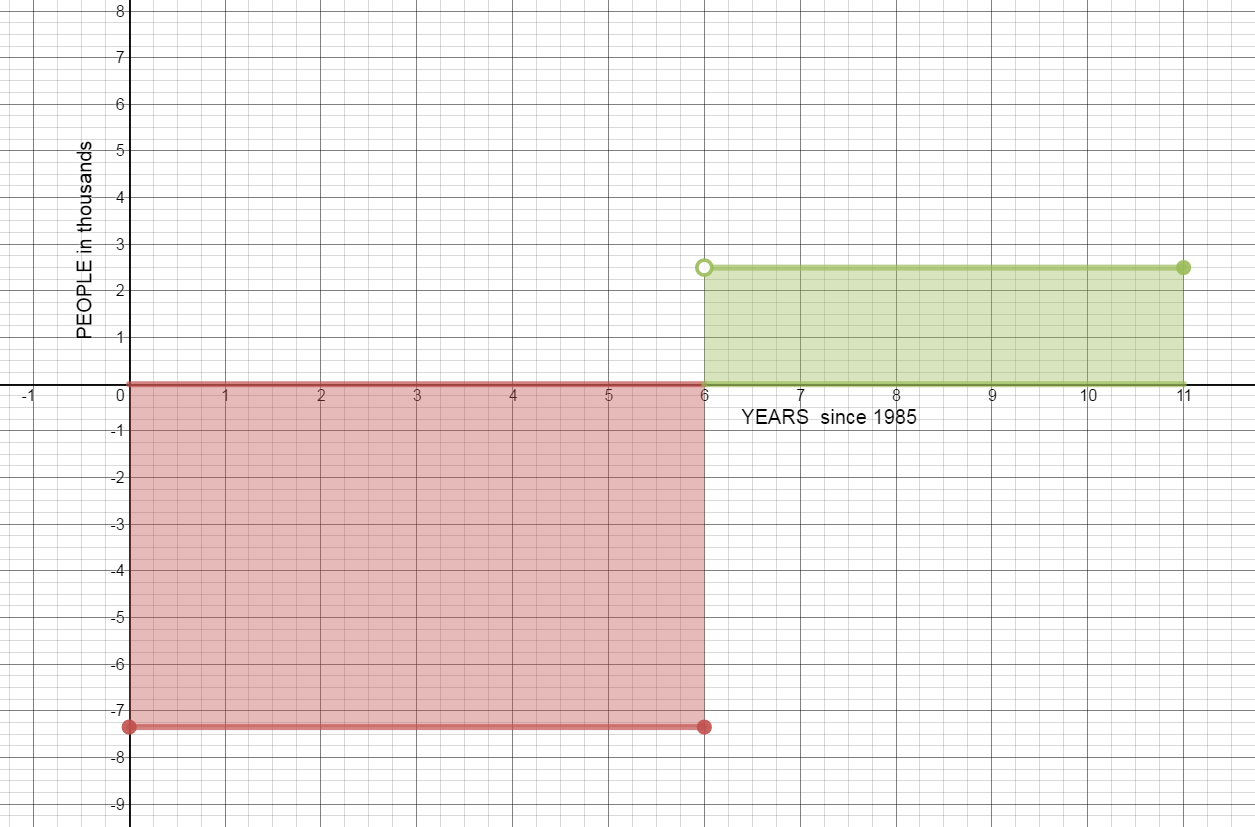
      Graph of Change in Population of North Dakota. Two horizontal lines. Graph of y=-7.35 from x=0 to x=6. Graph of y=2.5 from x>6 to x=11.

    2. Find the area of the region between the graph of p and the horizontal axis from 0 to 6. Interpret your answer.

      $A=lw$

      $A=7.35(6)$

      $A=44.1$

      There was a 44.1 thousand person decrease in population between 1985 and 1991.

    3. Find the area of the region between the graph of p and the horizontal axis from 6 to 11. Interpret your answer.

      $A=lw$

      $A=2.5(5)$

      $A=12.5$

      There was a 12.5 thousand person increase in population between 1991 and 1996.

    4. Was the population of North Dakota in 1996 greater or less than the population in 1985? By how much did the population change between 1985 and 1996?

      $-44.1+12.5=-31.6$

      In 1996 the population of North Dakota was 31.6 thousand people fewer than in 1985.

    5. What information would you need to determine the population of North Dakota in 1996?

      We need to know the population of North Dakota in 1985. If we know the population count for 1985, we can calculate the population in 1996 by subtracting 31,600 from the 1985 population count.

    6. What is the relationship between the area of the regions and the population of North Dakota?

      Each area represents the total change in population for the time period.

       

  2. An office worker assembles advertising portfolios. As fatigue sets in, the number of portfolios he can assemble per hour decreases. Using regression, it is determined that he can assemble $f\left( t \right) = 20 - {t^2}$ portfolios per hour $t$ hours after he begins work.

    1. How many portfolios can he assemble in the third hour?

      $f(3) = 20 - {\left( 3 \right)^2} = 20 - 9 = 11$

      The office worker assembles 11 portfolios in the third hour.

    2. Graph the equation on the interval [0,3] on the graph below and approximate the area under the curve using three left rectangles. Blank first quadrant graph

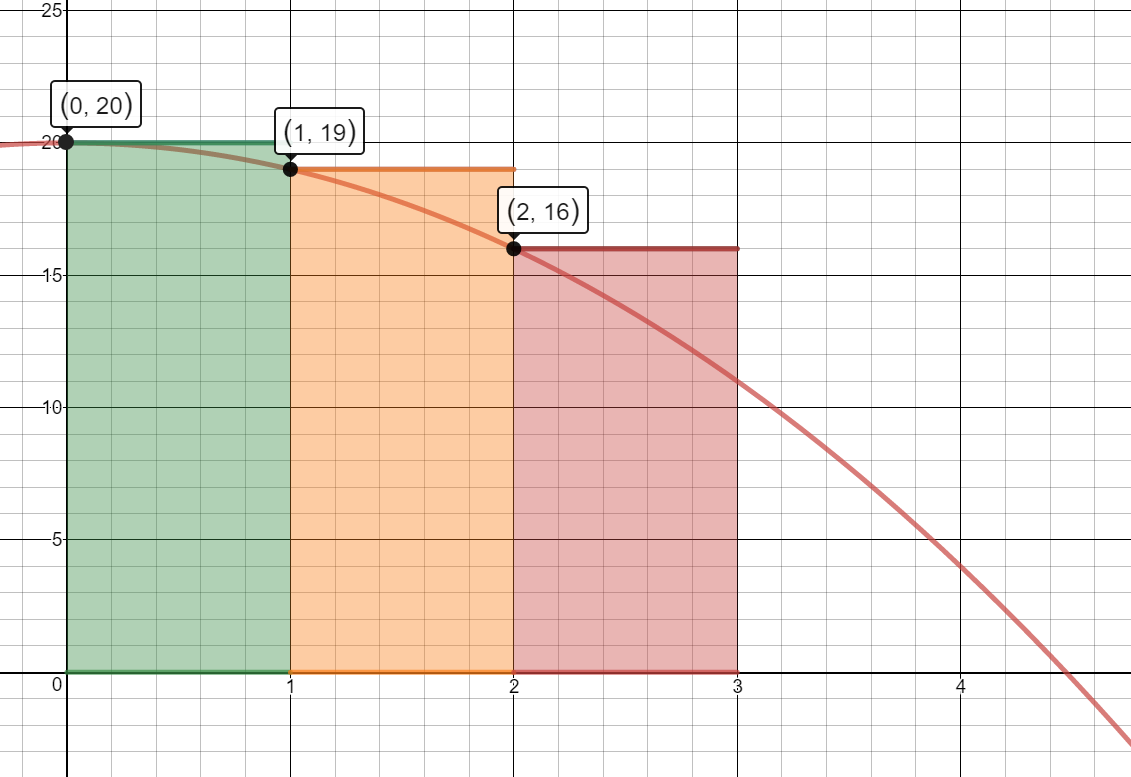
      y= 20 minus t sqaured graphed on the interval from 0 to 3 with left rectangles drawn that intersect the graph at (0, 20), (1,19), and (2,16)

      3 Left Rectangles

      $A\approx A1 + A2 + A3=1[f(0)] + 1[f(1)] + 1[f(2)]$

      $A\approx1(20) + 1(19) + 1(16)$

      $A\approx 20+19+16$

      $A\approx 55$

      The worker can assemble approximately 55 portfolios in 3 hours.

    3. Find the area under the curve using 6 left rectangles and then 9 left rectangles.

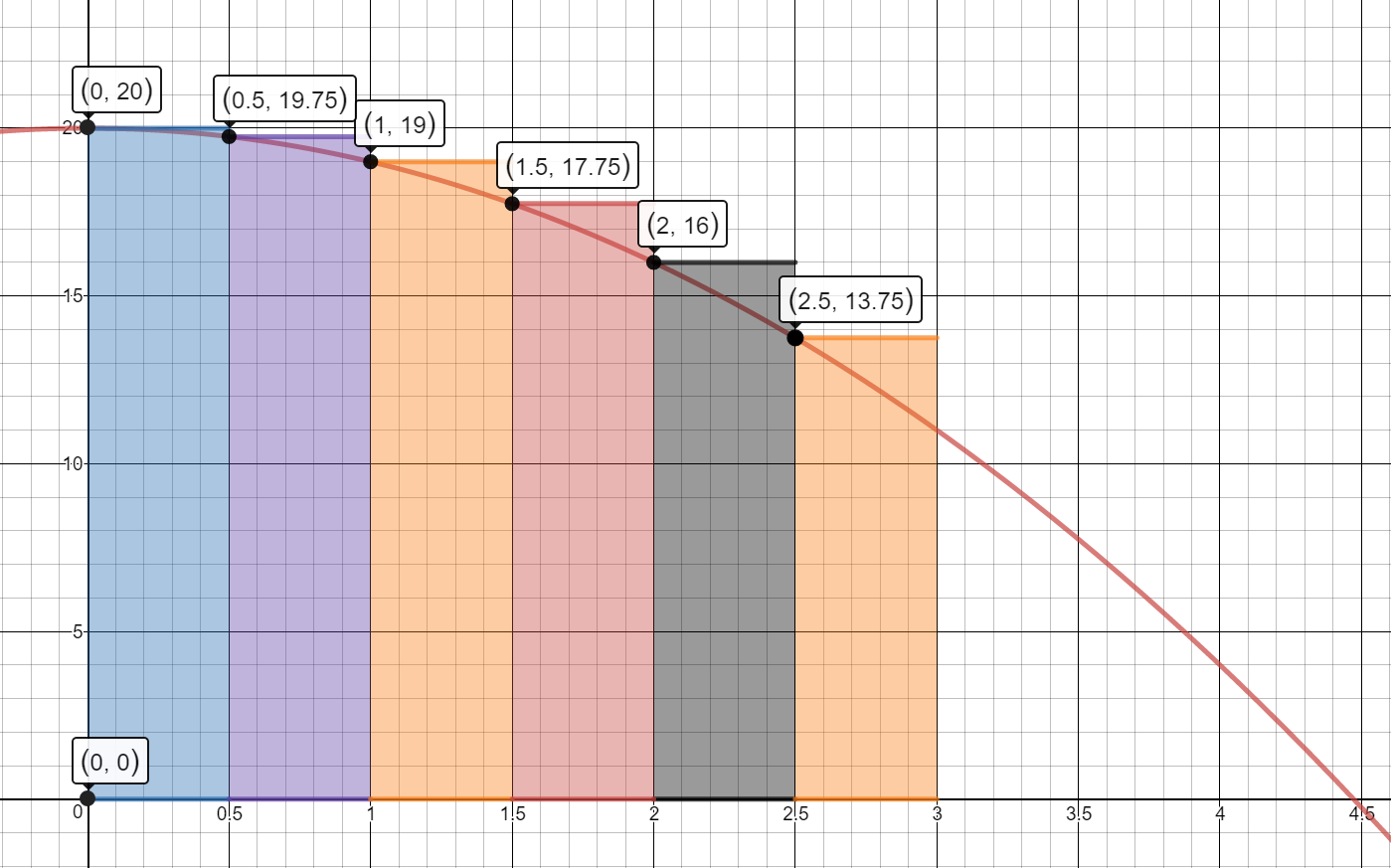
      y= 20 minus t sqaured graphed on the interval from 0 to 3 with left rectangles drawn that intersect the graph at (0, 20), (0.5, 19.75),(1,19),(1.5,17.75), (2,16) and (2.5,13.75)

      6 Left Rectangles

      $A \approx A1 + A2 + A3 + A4 + A5 + A6$

      $A \approx .5[f(0)] + .5[f(.5)] + .5[f(1)] + .5[f(1.5)] + .5[f(2)] + .5[f(2.5)]$

      $A\approx.5(20) + .5(19.75) + .5(19) + .5(17.75) + .5(16) + .5(13.75)$

      $A\approx10 + 9.875 + 9.5 + 8.875 + 8 + 6.875$

      $A\approx53.125$

      The worker can assemble approximately 53.125 portfolios in 3 hours.

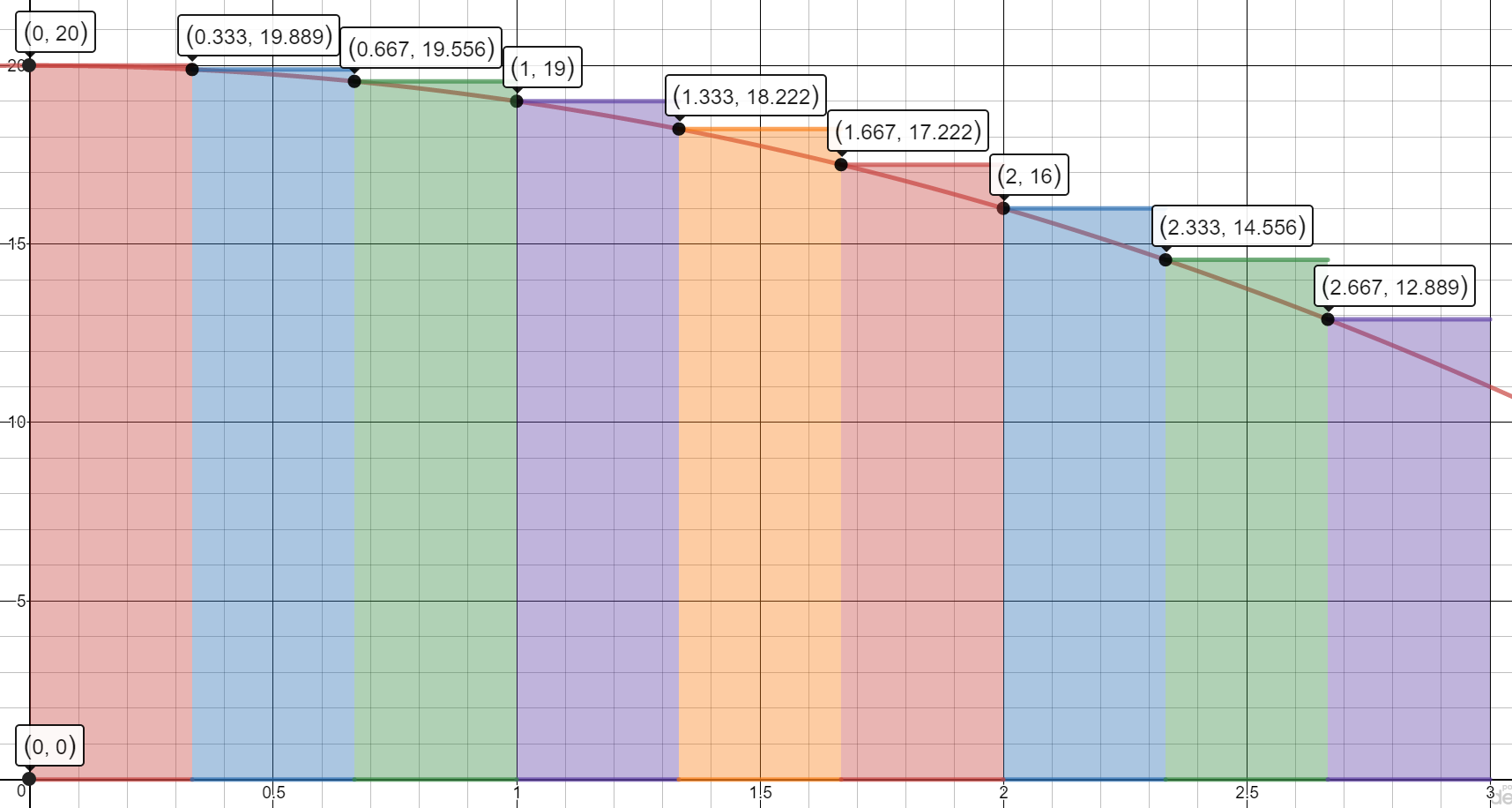
      y= 20 minus t sqaured graphed on the interval from 0 to 3 with left rectangles drawn that intersect the graph at (0, 20), (0.333, 19.889), (0.667, 19.556),(1,19),(1.333, 18.222), (1.667, 17.222), (2,16) and (2.333, 14.556), (2.667,12.889)

      9 Left Rectangles

      A \approx A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8 + A9

      $A \approx \frac{1}{3}[f(0)] + \frac{1}{3}[f(\frac{1}{3})] + \frac{1}{3}[f(\frac{2}{3})] + \frac{1}{3}[f(1)] + \frac{1}{3}[f(\frac{4}{3})]+ \frac{1}{3}[f(\frac{5}{3})] + \frac{1}{3}[f(2)] + \frac{1}{3}[f(\frac{7}{3})] + \frac{1}{3}[f(\frac{8}{3})]$

      $A\approx\frac{1}{3}(20) + \frac{1}{3}(19.889) + \frac{1}{3}(19.556) + \frac{1}{3}(19) + \frac{1}{3}(18.222)+ \frac{1}{3}(17.222) + \frac{1}{3}(16) + \frac{1}{3}(14.556) + \frac{1}{3}(12.889)$

      $A\approx52.444$

      The worker can assemble approximately 52.444 portfolios in 3 hours.

    4. Do you think using 3 or 6 or 9 rectangles is a more accurate measure of the area? What could you do to get an even better measure?

      Using 9 rectangles is the more accurate measure of the area. We would get even an even better measure of the area if we used more rectangles.

    5. What does the area under the curve represent?

      The area under the curve represents the total number of portfolios the worker can assemble in the given time period.

Notes

  1. Estimate the area under the curve $f(x) = {x^2}$ on the domain [0,4] by summing the areas of the four Right Hand Rectangles. Is your estimate greater than the actual area or less than the actual area?

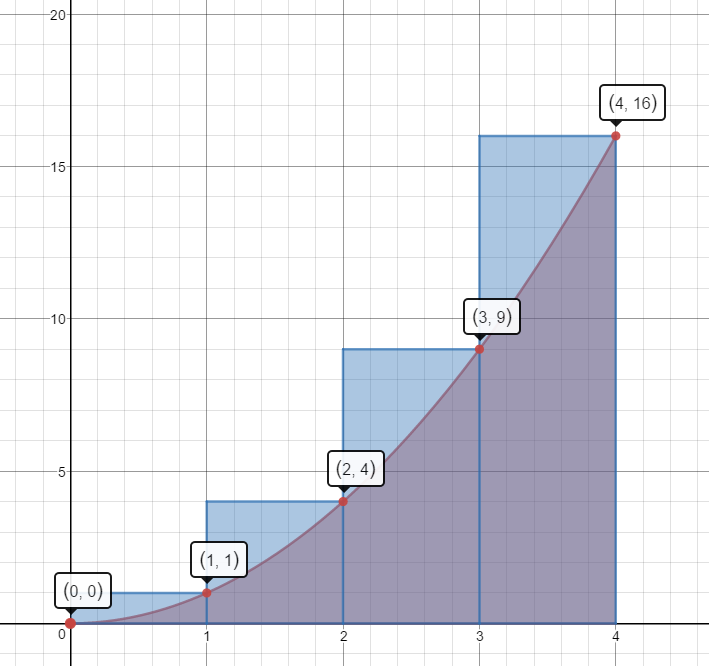
    Graph of y=x squared on the interval from x=0 to x=4 with right-rectangles drawn

    $A\approx 1(1)+1(4)+1(9)+1(16)=1+4+9+16=30\;units^2$

    This estimate is more than the actual area.

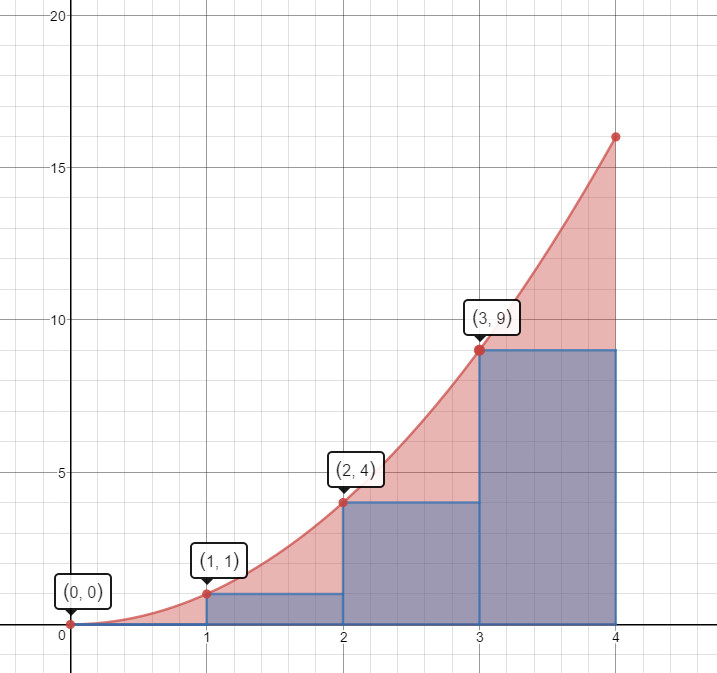
    Graph of y=x squared on the interval from x=0 to x=4 with left-rectangles drawn

    Left Hand Rectangles

    $A\approx1(0)+1(1)+1(4)+1(9)=0+1+4+9=14\;units^2$

    This estimate is less than the actual area.

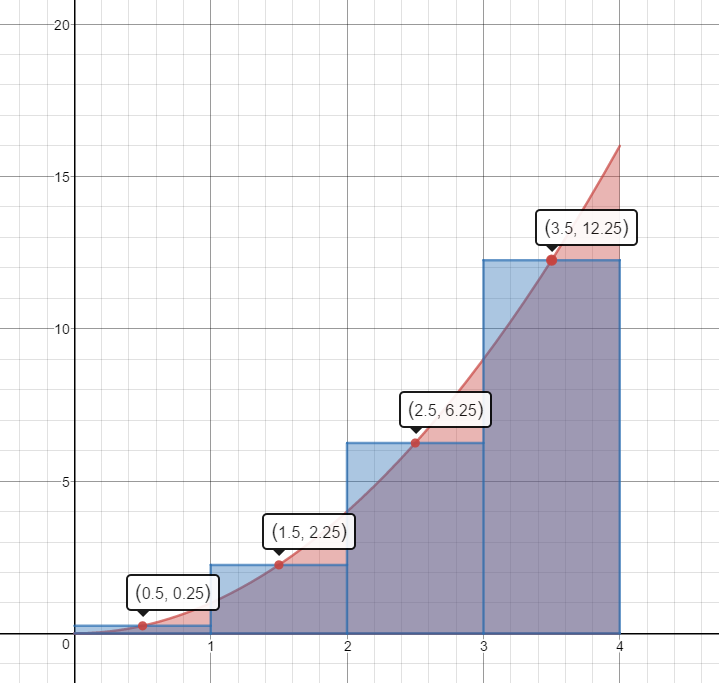
    Graph of y=x squared on the interval from x=0 to x=4 with midpoint-rectangles drawn

    Mid-Point Rectangles

    $A\approx 1(.25)+1(2.25)+1(6.25)+1(12.25)=.25+2.25+6.25+12.25=21\;units^2$

    This estimate is slightly less than the actual area.

  2. Use 3 Right Hand Rectangles to estimate the area under the curve $f(x) = 2x$ on the domain [1,4].

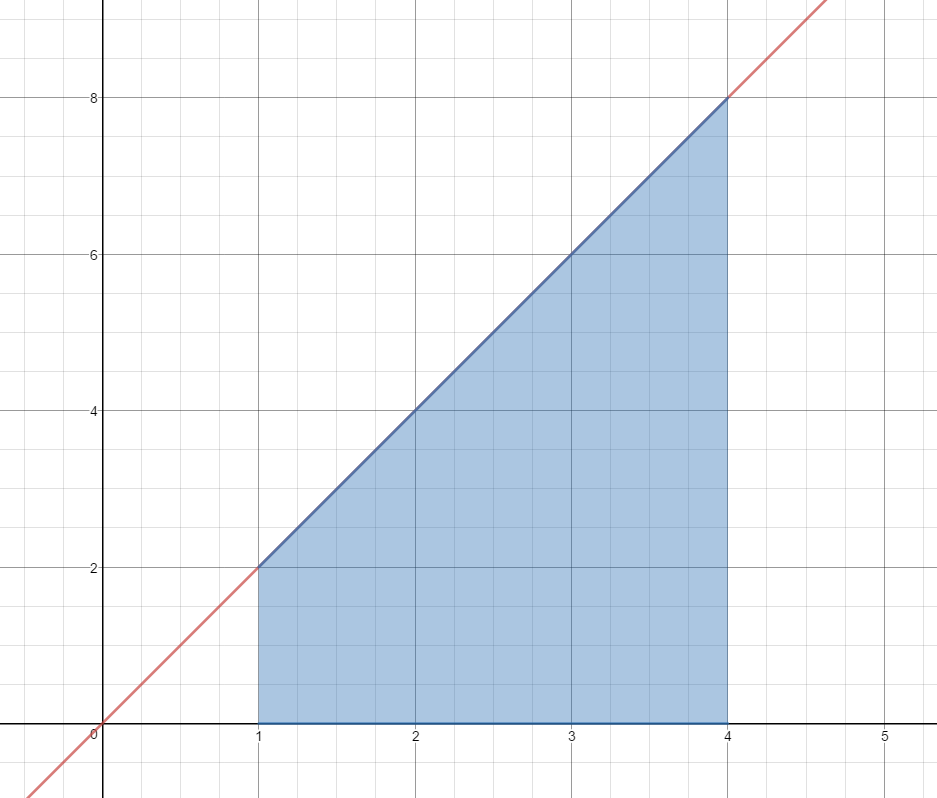
    Graph of y=2x on the interval from x=1 to x=4

    $A\approx1(4)+1(6)+1(8)$

    $A\approx4+6+8$

    $A\approx 18\;units^2$

    Is this estimate less than the actual area or greater than the actual area?

    This estimate is more than the actual area.

  3. Use 3 Mid-Point Rectangles to estimate the area under the curve $f(x) = {x^3}$ on the domain [1,4].

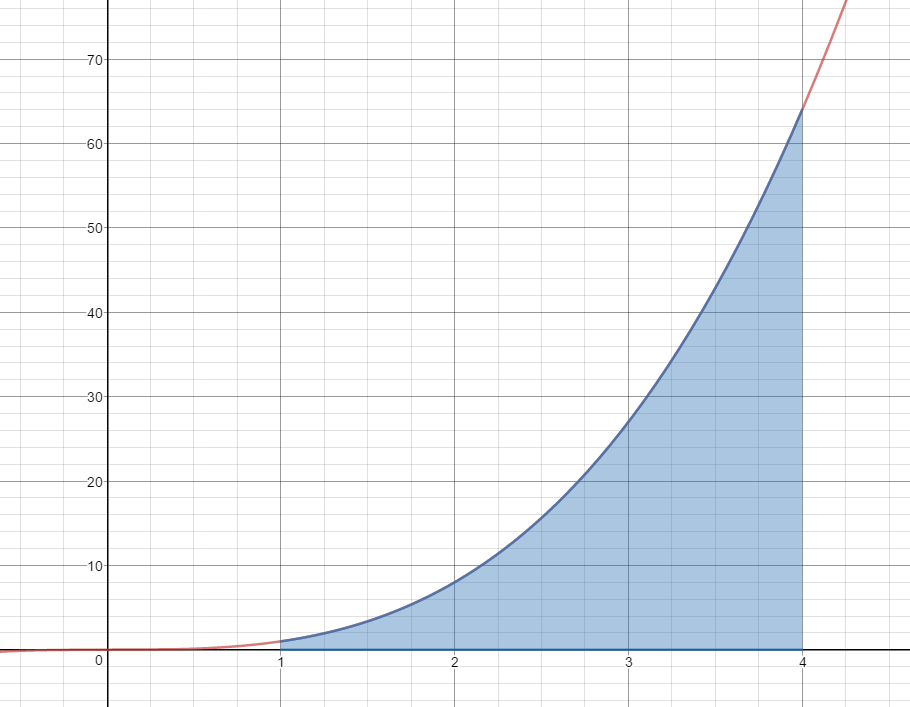
    Graph of y=x cubed on the interval from x=1 to x=4

    $A\approx 1{(1.5)^3} + 1{(2.5)^3} + 1{(3.5)^3}$

    $A\approx 3.375 + 15.625 + 42.875$

    $A\approx 61.875\;units^2$

    Is this estimate less than the actual area or greater than the actual area?

    This estimate is less than the actual area.

  4. Use 3 Left Hand Rectangles to estimate the area under the curve $f(x) = \frac{1}{x}$ on the domain [0.5, 2.0].

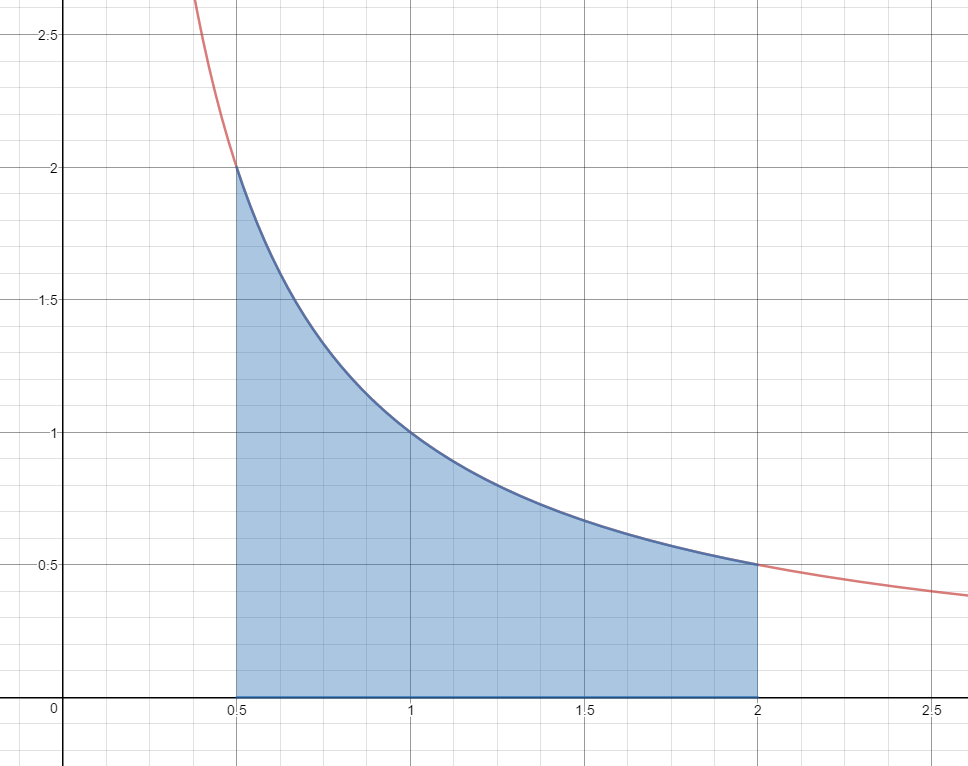
    Graph of y=1/x on the interval from x=0.5 to x=2.0

    $A\approx \frac{1}{2}\left( {\frac{1}{{.5}}} \right) + \frac{1}{2}\left( {\frac{1}{1}} \right) + \frac{1}{2}\left( {\frac{1}{{1.5}}} \right)$

    $A\approx \frac{1}{2}(2) + \frac{1}{2}(1) + \frac{1}{2}\left( {\frac{2}{3}} \right)$

    $A\approx 1 + \frac{1}{2} + \frac{1}{3}$

    $A\approx 1.83\;units^2$

    Is this estimate less than the actual area or greater than the actual area?

    This estimate is greater than the actual area.

4.1 Area by Sums

Practice

  1. A person walking along a straight path has her velocity in miles per hour at time t given by the function $$v(t)=0.25{{t}^{3}}-1.5{{t}^{2}}+3t+0.25,$$ for times in the interval $0\le t\le 2$. The graph of this function is also given in each of the three diagrams below.

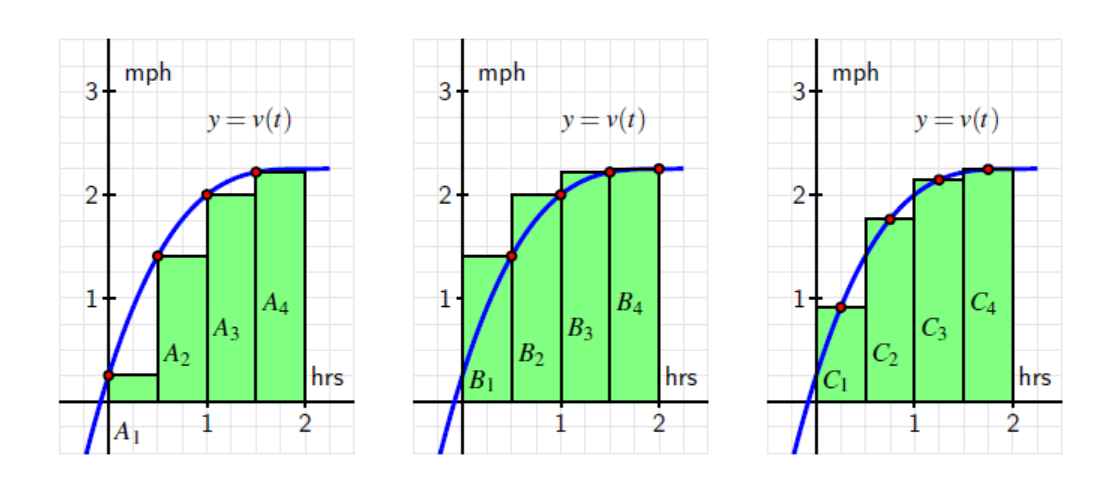
    enter image description here
    1. Estimate the area under each of the curves by summing the areas of the rectangles.

      Left Rectangles: $A_1+A_2+A_3+A_4$

      $.5(.25)+.5(1.4063)+.5(2)+.5(2.2188)=2.93755$

      Right Rectangles: $B_1+B_2+B_3+B_4$

      $.5(1.4063)+.5(2)+.5(2.2188)+.5(2.25)=3.93755$

      Midpoint Rectangles: $C_1+C_2+C_3+C_4$

      $.5(.91)+.5(1.7617)+.5(2.1445)+.5(2.2461)=3.53115$

    2. Why are the three answers different?

      Each estimates the area under the curve using different size rectangles.

    3. Of the three estimates from part a, which do you think is the best approximation of the area under the curve?

      Using midpoints gives the best approximation.

    4. How could you get a better approximation for the area under the curve?

      We would get a better approximation if we used more rectangles.

    5. What does the area under the curve represent?

      The area under the curve represents the total distance walked: $\frac{miles}{hour}\ast hour=miles.$

    Source: Active Calculus by Matthew Boelkins is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. Based on a work at http://scholarworks.gvsu.edu/books/10/.

  2. Given the function $f(x)=4-0.16{{x}^{2}}$,

    enter image description here approximate the area under the curve on the interval [0, 6] using 6 right rectangles.

    $A \approx 1[f(1)]+1[f(2)]+1[f(3)]+1[f(4)]+1[f(5)]+1[f(6)]$

    $A \approx 1(3.84)+1(3.36)+1(2.56)+1(1.44)+1(0)+1(-1.76)$

    $A\approx 9.44\;unit{{s}^{2}}$

  3. The rate of change of per capita consumption of a certain type of cheese in the United States from 1982 through 2002 can be modeled as $$C'\left( x \right)=-0.0011{{x}^{2}}+0.02x+0.2399$$ pounds per person per year where $x$ is the number of years since 1970.

    enter image description here
    1. According to the graph of $C'(x)$, when was the per capita consumption of this cheese growing and when was it declining?

      Growing: 1982 to about half way thru 1996

      Declining: mid-1996 through 2002

    2. Find the point of the graph of $C'(x)$ that corresponds to the time when the per capita consumption of this cheese, $C(x)$, was the greatest. Explain.

      Per capita consumption greatest at $x=26.43$ years or sometime in 1996

    3. Estimate using 7 right rectangles the area lying above the x-axis and below the graph of $C'(x)$ over the interval in part a. Interpret your answer.

      $A\approx2(.0343)+2(.2783)+2(.2435)+2(.1999)+2(.1475)+2(.0863)+2(.0163)=2.5522$

      Total per capita consumption of this cheese grew by 2.5522 pounds per person from 1982 to mid 1996.

    4. Estimate using 3 right rectangles the area lying below the x-axis and above the graph of $C'(x)$ over the interval in part a. Interpret your answer.

      $A\approx 2(-.0625)+2(-.1501)+2(-.2465)=-.9182$

      Total per capital consumption of this cheese decreased by .9182 pounds per person from mid 1996 to 2002.

    5. By how much did the per capita consumption of this cheese change between 1982 and 2002?

      $2.5522-.9182=1.634$

      Per capita consumption of this cheese grew by 1.634 pounds per person from 1982-2002.

    6. What information do we need to determine the per capita consumption of this cheese in 2002?

      We would need the actual per capita consumption in 1981 in order to determine the per capita consumption for any other year in the domain of the function.

Additional Resources