MATH 1830 Notes

Unit 3 Applications of Derivatives

3.5 Absolute Extrema

Pre-Class:

Complete 3.4 NearPod Activity, if you did not complete it in class.
Take notes on the videos and readings (use the space below).
Complete the 3.5 Pre-Class Quiz.

Read

Watch

3.5 Quiz

Introduction

On the following page, each member of the group is to draw 3 functions f(x) over an interval $a < x < b$.

Be creative! Try to draw as many different possibilities as you can.

I have drawn one for you as an example.

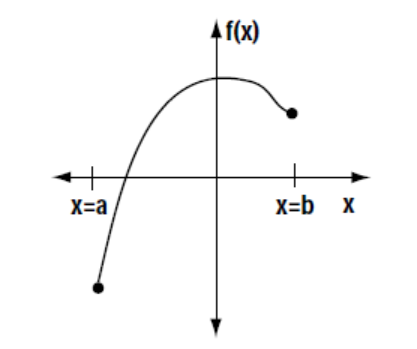
Sample Graph with Endpoints. Graph of f(x) on the interval from x=a to x=b.

Label each of your graphs (ex: graph #1, graph #2, etc).

For each of your graphs, answer the following questions:

Where does f (x) have its maximum value? That is, where on your graph does y have the largest value?
Where does f (x) have its minimum value?

Clearly indicate the answers to these two questions on each graph.
Based on your answers above, can your group arrive at a conclusion?
1. Could you make a general statement about how to determine the absolute maximum or minimum values of a function over a given interval?
2. Can you think of any exceptions?
3. How can our knowledge of derivatives assist us?
4. Summarize your responses on this sheet. Be prepared to share your results with the rest of the class.

Norris, Ken. (1999). Optimization Problems. Retrieved from https://www.stf.sk.ca/portal.jsp?Sy3uQUnbK9L2RmSZs02CjV/Lfyjbyjsxsd+sU7CJwaIY=F

Notes

Algorithm for Determining Extreme Values

Suppose that $f(x)$ is a continuous function over a closed interval [a, b].

To find the absolute maximum and minimum values of the function $f(x)$ on [a, b]:

Find $f'(x)$.
Determine the additional points to test in the interval [a, b].
(that is, find all x values for which $f'(x)=0$ (critical points), $f'(x)$ does not exist (possible cusps, etc.).
Create a table for (x, y) coordinates and list all $x$ values you plan to check: the endpoints $a,$ $b,$ and all critical values, possible cusps, etc.
Find the function values of all the $x$ values in the table.

The largest of these values is the absolute maximum of on the interval [a, b].
The smallest of these is the absolute minimum of on the interval [a, b].

Find the absolute minimum and maximum values of the function, if they exist, over the given interval.

$f(x)={{x}^{2}}-6x-3\quad \quad [-1,5]$

$ f'(x)=2x-6 $

Criticals: $f'(x)=0 $

$ 2x-6=0 $

$ 2x=6 $

$ x=3 $

Calculate $f(x)$ for the interval endpoints: ($x=-1, 5$), and critical values: ($x=3$).

$x$	$f(x)$
-1	$ 4$
3	$ -12 $
$5$	$ -8 $

The Absolute Maximum on the interval is: $(-1, 4)$.

The Absolute Minimum on the interval is: $(3, -12)$.

$f(x)=2{{x}^{3}}-3{{x}^{2}}-36x+62\quad \quad [-3,4]$

$ f'(x)=6{{x}^{2}}-6x-36 $

$ 6{{x}^{2}}-6x-36=0 $

$ 6\left( {{x}^{2}}-x-6 \right)=0 $

$ 6(x+2)(x-3)=0 $

$ x=-2$, and $x=3$

Calculate $f(x)$ for the interval endpoints: ($x=-3$ and $x= 4$), and critical values: ($x=-2$ and $x=3$).

$x$	$f(x)$
-3	$ 89$
-2	$106 $
3	$-19 $
4	$-2$

The Absolute Maximum on the interval is: $(-2, 106)$.

The Absolute Minimum on the interval is: $(3, -19)$.

$f(x)=x+\frac{1}{x}\quad \quad [1,20]$

$ f(x)=x+{{x}^{-1}} $

$ f'(x)=1+(-1){{x}^{-2}} $

$ f'(x)=1-\frac{1}{{{x}^{2}}} $

$ 0=1-\frac{1}{{{x}^{2}}} $

$ \frac{1}{{{x}^{2}}}=1 $

$ {{x}^{2}}=1 $

$ \sqrt{{{x}^{2}}}=1 $

$ x=1\text{ and }x=-1 $

Calculate $f(x)$ for the interval endpoints: ($x=1$ and $x=-1$), and critical values: ($x=20$).

Do not include the critical value $x=-1$ because it is not in interval.

$x$	$f(x)$
$1$	$2$
$20$	$20.05$

The Absolute Maximum on the interval is: $(20, 20.05)$.

The Absolute Minimum on the interval is: $(1, 2)$.

$f(x)=\frac{{{x}^{2}}}{{{x}^{2}}+1}\quad \quad [-2,2]$

$ f'(x)=\frac{({{x}^{2}}+1)(2x)-{{x}^{2}}(2x)}{{{\left( {{x}^{2}}+1 \right)}^{2}}} $

$ f'(x)=\frac{2{{x}^{3}}+2x-2{{x}^{3}}}{{{\left( {{x}^{2}}+1 \right)}^{2}}} $

$ f'(x)=\frac{2x}{{{\left( {{x}^{2}}+1 \right)}^{2}}} $

$ \frac{2x}{{{\left( {{x}^{2}}+1 \right)}^{2}}}=\frac{0}{1} $

$ 2x=0 $

$ x=0 $

Calculate $f(x)$ for the interval endpoints: ($x=-2$ and $x=2$), and critical values: ($x=0$).

$x$	$f(x)$
$-2$	$0.8$
$0$	$0$
$2$	$0.8$

The Absolute Maxima on the interval are: $(2, 0.8)$ and $(-2, 0.8)$.

The Absolute Minimum on the interval is: $(0, 0)$.

$f(x)=\frac{x}{{{(x+9)}^{2}}}\quad \quad [-1,8]$

$ f'(x)=\frac{{{\left( x+9 \right)}^{2}}(1)-x(2)(x+9)(1)}{{{\left( x+9 \right)}^{4}}} $

$f'(x)=\frac{\left( x+9 \right)\left[ \left( x+9 \right)-2x \right]}{{{\left( x+9 \right)}^{4}}}$

$f'(x)=\frac{\left( x+9 \right)-2x}{{{\left( x+9 \right)}^{3}}}$

$f'(x)=\frac{-x+9}{{{\left( x+9 \right)}^{3}}} $

$ \frac{-x+9}{{{\left( x+9 \right)}^{3}}}=\frac{0}{1} $

$ -x+9=0 $

$ 9=x $

Calculate $f(x)$ for the interval endpoints: ($x=-1$ and $x=8$).

Do not include the critical value $x=9$ because it is not in the interval.

$x$	$f(x)$
$-1$	$-0.0156$
$8$	$0.0227$

The Absolute Maximum on the interval is: $(8, 0.0277)$.

The Absolute Minimum on the interval is: $(-1, -0.0156)$.

$f(x)=-3\quad \quad [-2,2]$

$f'(x)= 0$

$x$	$f(x)$
$-2$	$-3$
$2$	$-3$

There are no maximum or minimum values because this is a constant function.

An employee’s monthly production $M$, in number of units produced, is found to be a function of the number of year of service, $t$. For a certain product, a productivity function is given by: $M(t)=-2{{t}^{2}}+100t+180,\quad 0\le t\le 40$

Find the maximum productivity and the year in which it is achieved.

$M'(t)=-4t+100$

$ -4t+100=0$

$t=25$

Calculate $M(t)$ for the interval endpoints: ($t=0, 40$), and critical values: ($t=25$).

$t$	$M(t)$
0	$180$
25	$1430$
40	$980$

The maximum monthly productivity is 1430 units per month in year 25 of service.

A firm determines that its total profit in dollars from the production and sale of x thousand units of a product is given by: $$P(x)=\frac{1500}{{{x}^{2}}-6x+10}\quad \quad x\ge 0$$

Find the number of units x for which the total profit is a maximum.

Note: this function is continuous on the interval $\left(0,\infty\right).$

$ P'(x)=\frac{\left( 0 \right)\left( {{x}^{2}}-6x+10 \right)-1500\left( 2x-6 \right)}{{{\left( {{x}^{2}}-6x+10 \right)}^{2}}} $

$ P'(x)=\frac{-3000x+9000}{{{\left( {{x}^{2}}-6x+10 \right)}^{2}}} $

$ \frac{-3000x+9000}{{{\left( {{x}^{2}}-6x+10 \right)}^{2}}}=\frac{0}{1} $

$ -3000x+9000=0$ therefore$ x=3 $

Calculate $P(x)$ for the interval endpoint: ($x=0$), and critical value: ($x=3$). Note, we were not given an upper interval endpoint. Test one point beyond $x=3$ to identify the behavior of $P(x)$ for values of $x$ greater than the critical value of $x=3$. We will use $x=5$. Your answer will not include both a maximum and a minimum because the interval is open on one end.

$x$	$P(x)$
$0$	$150$
$3$	$1500$
$5$	$300$

Because the graph is decreasing for $x$ values greater than $3$, we have an Absolute Maximum at $(3,1500)$ but no Absolute Minimum.

The profit is maximized at $1500 when 3000 units are sold.

Norris, Ken. (1999). Optimization Problems. Retrieved from https://www.stf.sk.ca/portal.jsp?Sy3uQUnbK9L2RmSZs02CjV/Lfyjbyjsxsd+sU7CJwaIY=F

3.5 Absolute Maximum and Absolute Minimum

Practice

Find the absolute minimum and maximum values of the function, if they exist, over the given interval.

$f(x)={{x}^{3}}-3x+6\quad \quad [-2,2]$

$f'(x)=3{{x}^{2}}-3$

$ 3{{x}^{2}}-3=0$

$ {{x}^{2}}=1$

$ x=\pm 1$

$x$	$f(x)$
$-2$	$4$
$-1$	$8$
$1$	$4$
$2$	$8$

In the interval, the function has an Absolute Minimum at the point: $(-2, 4)$ and $(1, 4).$

In the interval, the function has an Absolute Maximum at the point: $(-1, 8)$ abd $(2, 8).$

$y={{x}^{4}}-4{{x}^{3}}\quad \quad [-4,6]$

$y'=4{{x}^{3}}-12{{x}^{2}}$

$ 4{{x}^{3}}-12{{x}^{2}}=0$

$ 4{{x}^{2}}(x-3)=0$

$ 4{{x}^{2}}=0\quad x-3=0$

$ x=0\quad \quad x=3$

$x$	$y$
$-4$	$512$
$0$	$0$
$3$	$-27$
$6$	$432$

In the interval, the function has an Absolute Minimum at the point: $(3, -27).$

In the interval, the function has an Absolute Maximum at the point: $(-4, 512).$

$y=\frac{{{x}^{2}}}{3x-6}\quad \quad [3,6]$

$ y'=\frac{\left( 3x-6 \right)(2x)-{{x}^{2}}(3)}{{{\left( 3x-6 \right)}^{2}}} $

$y'=\frac{6{{x}^{2}}-12x-3{{x}^{2}}}{{{\left( 3x-6 \right)}^{2}}}$

$ y'=\frac{3{{x}^{2}}-12x}{{{\left( 3x-6 \right)}^{2}}} $

$ \frac{3{{x}^{2}}-12x}{{{\left( 3x-6 \right)}^{2}}}=\frac{0}{1} $

$ 3{{x}^{2}}-12x=0 $

$ 3x(x-4)=0 $

$ 3x=0\quad x-4=0 $

$ x=0\quad \quad x=4 $

0 is not in interval.

$x$	$y$
$3$	$3$
$4$	$2.7$
$6$	$3$

In the interval, the function has an Absolute Minimum at the point: $(4, 2.7).$

In the interval, the function has two Absolute Maxima at the points: $(3, 3)$ and $(6, 3).$

$y=\left(x+2\right)^{2/3}\quad \quad [-4,-2]$

$ y'=\frac23\left(x+2\right)^{-1/3}(1) $

$ y'=\frac2{3(x+2)^{1/3}}$

$ y'=\frac{2}{3\sqrt[3]{x+2}} $

$ \frac{2}{3\sqrt[3]{x+2}}=\frac{0}{1} $

$ 2=0 $

No critical numbers

$x$	$y$
$-4$	$1.59$
$-2$	$0$

In the interval, the function has an Absolute Minimum at the point: $(-2, 0).$

In the interval, the function has an Absolute Maximum at the point: $(-4, 1.59).$

Find the absolute minimum and maximum values of the function, if they exist, over the given interval.

$g(x)=\frac13x^3-2x-2\;\;\;\;\left[-2,3\right]$

$g'(x)=x^2-2$

$ {{x}^{2}}-2=0 $

$ x=\sqrt{2},x=-\sqrt{2} $

$x$	$g(x)$
$-2$	$-.67$
$-1.414$	$-.11$
$1.414$	$-3.89$
$3$	$1$

In the interval, the function has an Absolute Minimum at the point: $(1.414,-3.89).$

In the interval, the function has an Absolute Maximum at the point: $(3, 1).$

Would your answers in part a change if we considered [-2,2] instead?

$x$	$g(x)$
$-2$	$-.67$
$-1.414$	$-.11$
$1.414$	$-3.89$
$2$	$-3.33$

In the interval, the function still has an Absolute Minimum at the point: $(1.414, -3.89).$

In the interval, the function now has an Absolute Maximum at the point: $(-1.414, -.11).$

What if we changed the interval to $-2\le x\le 1$?

$x$	$g(x)$
$-2$	$-.67$
$-1.414$	$-.11$
$1$	$-3.67$

In the interval, the function now has an Absolute Minimum at the point: $(1, -3.67).$

In the interval, the function now has an Absolute Maximum at the point: $(-1.414, -.11).$

The temperature, T, of person during an illness is given by: $$T(t)=-0.1{{t}^{2}}+1.2t+98.6\ \ \ 0\le t\le 12$$ where T = temperature (°F) at time t, in hours since noon. Find the maximum value of the temperature and when it occurs.

$ T'(t)=-0.2t+1.2 $

$ -0.2t+1.2=0 $

$ -0.2t=-1.2 $

$ t=6 $

$t$	$T(t)$
$0$	$98.6$
$6$	$102.2$
$12$	$98.6$

In the interval, the maximum temperature of 102.2 degrees occurs at 6 pm.

Technicians working for the Ministry of Natural Resources have found that the amount of a pollutant in a certain river can be represented by $P(t)$ where $t$ is the time (in years) since a clean-up campaign started. At what time was the pollution at its lowest level?

$$P(t)=2t+\frac{1}{162t+1}\quad \quad 0\le t\le 1$$

$ P(t)=2t+{{\left( 162t+1 \right)}^{-1}} $

$ P'(t)=2+\left( -1 \right){{\left( 162t+1 \right)}^{-2}}\left( 162 \right) $

$ P'(t)=2-\frac{162}{{{\left( 162t+1 \right)}^{2}}} $

$ 2-\frac{162}{{{\left( 162t+1 \right)}^{2}}}=0 $

$ 2=\frac{162}{{{\left( 162t+1 \right)}^{2}}} $

$ \frac{2}{1}=\frac{162}{{{\left( 162t+1 \right)}^{2}}} $

$ 2{{\left( 162t+1 \right)}^{2}}=162 $

$ {{\left( 162t+1 \right)}^{2}}=81 $

$ 162t+1=\pm 9 $

$ 162t+1=-9 $

$ t=-\frac{10}{162}=-\frac{5}{81}\text{ (not in the interval)} $

$ 162t+1=9 $

$ t=\frac{8}{162}=\frac{4}{81} $

$t$	$P(t)$
$0$	$1$
$\frac4{81}$	$0.21$
$1$	$2.01$

$\left( \frac{4}{81} \right)(365\; days)=18.02$

The pollution was at its lowest level 18 days after clean up began.

Norris, Ken. (1999). Optimization Problems. Retrieved from https://www.stf.sk.ca/portal.jsp?Sy3uQUnbK9L2RmSZs02CjV/Lfyjbyjsxsd+sU7CJwaIY=F