MATH 1830

Unit 1 Limits

1.3 Continuity

Pre-Class:

1.2 HW

Read

Watch

1.3 Quiz

Resources

Introduction

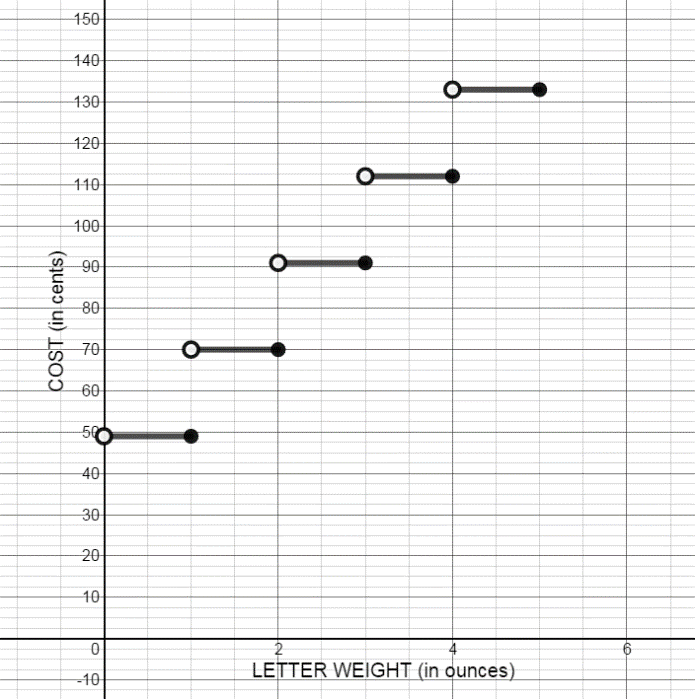
  1. The table below shows the cost of mailing a letter that weighs x ounces.

    Weight Cost
    0 < x ≤ 1 49¢
    1 < x ≤ 2 70¢
    2 < x ≤ 3 91¢
    3 < x ≤ 4 112¢
    4 < x ≤ 5 133¢
    1. Complete the table of letters with the following weights.
      Weight Cost
      .98

      49
      1.26

      70
      2.55

      91
      3.01

      112
      4.29

      133
    2. Graph the function. 1st quadrant coordinate plane with wieght on the x-axis and cost on the y-axis. Weight is measured in ounces and marked in intervals of one. Cost is measured in cents and marked in intervals of 20 cents.

      enter image description here

    Source http://www.stamps.com/usps/postage-rate-increase/

  2. Given: $f(x) = \frac{{3{x^2} - 12x - 15}}{{{x^2} - 3x - 10}}$

    1. From looking at the given function (and NOT graphing), where would you expect to see vertical asymptote(s)?

      $f(x) = \frac{{3{x^2} - 12x - 15}}{{{x^2} - 3x - 10}} = \frac{{3{x^2} - 12x - 15}}{{\left( {x - 5} \right)\left( {x + 2} \right)}}$

      Expect the vertical asymptotes to be located at x value where the denominator is equal 0, and the numerator is equal some number other than zero. There are possibly vertical asymptotes at $x = 5$ and $x = -2$.

    2. Graph the function. Where are the vertical asymptote(s)?

      Blank coordinate plane. Origin in the middle of the graph. Ten lines each to the left, right, above and below the origin.

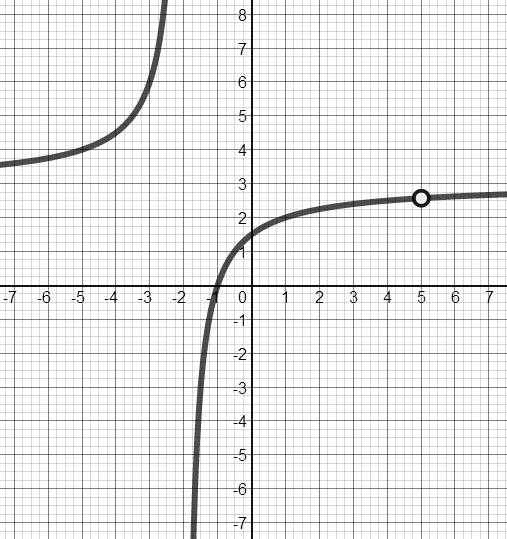
      Graph of (3x squared-12x-15) divided by (x squared-3x-10). Asymptote at x=-2. Hole at x=5. Horizontal asymptote at y=3.

      Vertical Asymptote at x = - 2 and a hole at x = 5.

    3. Do you get the same answer for a & b? Why or why not?

      There was a hole at $x = 5$. If you factor the numerator AND the denominator, they both contain $(x - 5)$.

Notes

Informal Definition: Continuity

A function is continuous over an interval if the graph over the interval can be drawn without removing the pencil from the paper.

Formal Definition: Continuity

A function, f(x), is continuous at the point $x = c$ if all three of the following requirements are met:

  1. $\underset{x\rightarrow\ c}{lim} f\left( x \right)$ exists
  2. $f\left( c \right)$ exists
  3. $\underset{x\rightarrow\ c}{lim} f\left( x \right) = \;\;f\left( c \right)$

Examples of Continuous and Discontinuous Functions:

Graph of f(x)=-(1/2)(x-1)^2 + 3. Hole in graph of f(x) at x=1. With equation f(x) should be 3. Point at (1,2). Domain of graph [-1,4]

This function is discontinuous because the $\underset{x\rightarrow\ 1}{lim} f\left( x \right)$ and the point $f\left( 1 \right)$ are not equal.

Graph of f(x)=-(1/2)(x-1)^2 + 3. Point at (1,3) defined and all other poings in dpmain [-1,4] defined as (x, f(x0)

This function is continuous since the limit and the value at $x=1$ are equal.

Graph of f(x)=-(1/2)(x-1)^2 + 3. Hole in graph of f(x) at x=1. With equation f(x) should be 3. No other point for x=1 defined. Domain of graph [-1,4]

The function is discontinuous because the point $f\left( 1 \right)$ does not exist.

Active Calculus https://open.umn.edu/opentextbooks/

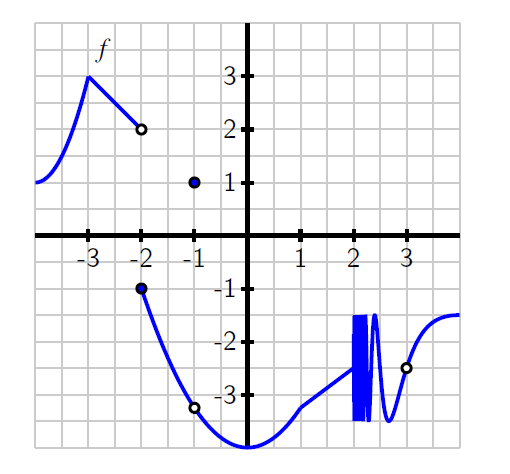
In Groups: Use the formal definition of continuity to discuss the continuity of the function whose graph is shown below.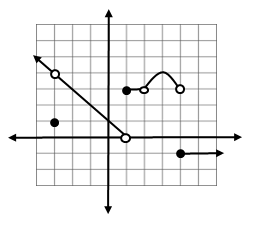

First Piece: y equals negative x plus 1. Domain: x is less than 1. Hole at point negative 3, four. Point at negative 3, one. Second Piece: y equals 3 on domain x is greater than or equal to 1 to x is less than 2. Third Piece: y is equal to negative (x -3) squared plus 4 on domain x is greater than 2 and less than 4. Fourth Piece: y equals negative 1 on domain x is greater than or equal to 4.

  1. Continuity at $x = - 3$

    Discontinuous @ $x = - 3.$ The $\underset{x\rightarrow-3}{lim} f(x)$ exists and the point $f( - 3)$ exists, but they are not equal.

  2. Continuity at $x = - 2$

    Continuous @ $x = - 2 \quad\ $ Satisfies all 3 requirements.

  3. Continuity at $x = 1$

    Discontinuous @ $x = 1 \quad\ \underset{x\rightarrow\ 1}{lim} f(x) \:\ $ DNE

  4. Continuity at $x = 2$

    Discontinuous @ $x = 2.$ The point $f(2)$ does not exist.

  5. Continuity at $x = 3$

    Continuous @ $x = 3 \quad\ $ Satisfies all 3 requirements.

  6. Continuity at $x = 4$

    Discontinuous @ $x = 4 \quad\ \underset{x\rightarrow\ 4}{lim} f(x) \:\ $ DNE

    Rules for Continuity

  1. $h\left( x \right) = 5 - 3x$

    Yes, because it is a polynomial function.

  2. $n\left( x \right) = \;\frac{{x - 3}}{{{x^2}\; + \;2x - 15}}$

    $n\left( x \right) = \;\frac{{x - 3}}{{(x + 5)(x - 3)}}$

    No, it is discontinuous at x=- 5 and x = 3.

  3. $f\left( x \right) = \;\sqrt {25 - {x^2}} $

    Continuous for $x: - 5 \le x \le 5$

  4. $g\left( x \right) = \;\sqrt[3]{{{x^2} - 4}}$

    Yes, continuous for all x because it is a function with an odd root.

1.3 Continuity

Practice

Below is a graph of $y=f(x)$. Use the graph to answer the following questions.

4 Quadrant coordinate plane. -4 to 4 on x- and y-axes. Graph description from left to right. At (-4,1) curve increases until (-3,3) where there is a sharp point and the graph decreases linearly until an open circle at (-2,2) where that part of the graph ends. The graph then begins again at a closed circle at (-2,-1) with a quadratic curve that goes until (1,-3.5) In that quadratic there is a hole at (-1,-3.5) and it has a y-intercept of (0,-4). In addition, there is a solid dot at the point (-1,1). The quadratic graph changes to linear at (1,-3.5) and increases until the point (2,-2.5). The graph then oscillates from x=2 to approximately x=2.5 in the range of y=-3.5 to y=-1.5. At x=2.5 the oscillation of the graph slows and the graph continues and increases until a hole at (3.-2.5). The graph then continues to increase and levels off at (4,-1.5)

  1. State all values of $x$ for which f is not continuous at $x=a$.

    (In other words, at what x values is the graph not continuous?)

    Discontinuous at $x=-2$ and $x=-1$ and $x=3.$

  2. At which values of $a$ does $\underset{x\rightarrow{a}}{lim}\,\ f(x)$ not exist?

    (In other words, where on this graph does the limit not exist?)

    The limit does not exist at $x=-2$ and $x=2.$

  3. At which values of $a$ does f have a limit, but $\underset{x\rightarrow{a}}{lim}\,\ f(x)\ne \ f(a)$?

    (In other words, where on the graph are the limit and the point not the same?)

    At $x=-1, f(-1)$ exists but $\underset{x\rightarrow{-1}}{lim}\,\ f(x)\ne \ f(-1).$

    At $x=3, f(3)$ does not exist.

  4. Which condition is stronger, and hence implies the other: f has a limit at $x = a$ or f is continuous at $x = a$? Explain.

    The statement f is continuous at $x = a$ is stronger.

    Based on your answer, choose the correct statement below :
    1. If f is continuous at $x = a$, then f has a limit at $x = a$
    2. If f has a limit at $x = a$, then f is continuous at $x = a$

      The correct statement is statement a: If f is continuous at $x = a$, then f has a limit at $x = a.$

      Because having a limit at $x = a$ is a requirement for continuity at $x = a$, but continuity at $x = a$ is not an requirement for having a limit at $x = a$.

    Active Calculus by Matthew Boelkins is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. Based on a work at http://scholarworks.gvsu.edu/books/10/.

Additional Resources