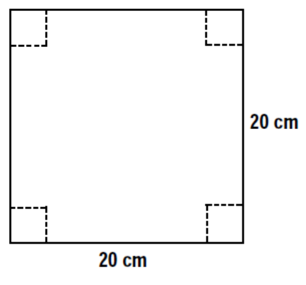
Write a mathematical function for each of the following and then find the requested information.
Be sure to include a properly labeled diagram (if applicable) and variable statements. State the restrictions on the independent variable.
-
When a theater owner charges \$3 for admission, there is an average attendance of 100 people. For every \$0.10 increase in admission, there is a loss of 1 customer from the average number. How much should the theater owner charge to maximize revenue and
what is the maximum revenue?
x=number of .10 cent increases in admission costs
$R(x)=$(price per ticket)(number of tickets sold)
$R(x)=(3+0.10x)(100-1x)$
$R(x)=300-3x+10x-0.1{{x}^{2}}$
$R(x)=300+7x-0.1{{x}^{2}}$
$R'(x)=7-0.2x$
$7-0.2x=0$
$7=0.2x$
$35=x$
Ticket Price= $3+.1x=3+.1(35)=6.50$
Revenue= $(3+.1(35))(100-35)=422.50$
The theatre owner should charge \$6.50 per ticket to have the maximum revenue of $422.50.
-
A Norman window is a rectangle with a semi-circle on top. Find the maximum area if the perimeter is 24 feet, express the area as a function of the radius (r).
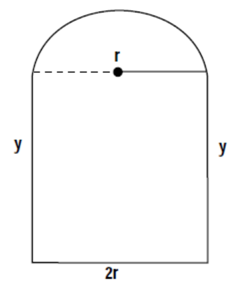
$P=2y+2r+\frac{1}{2}\left( 2\pi r \right)$
$24=2y+2r+\frac{1}{2}(2\pi r)$
$24=2y+2r+\pi r$
$\frac{24-2r-\pi r}{2}=y$
$A=l\cdot w+\frac{1}{2}\pi {{r}^{2}}$
$A=\left( \frac{24-2r-\pi r}{2} \right)2r+\frac{1}{2}\pi {{r}^{2}}$
$A=\left( 24-2r-\pi r \right)r+\frac{1}{2}\pi {{r}^{2}}$
$A=24r-2{{r}^{2}}-\pi {{r}^{2}}+\frac{1}{2}\pi {{r}^{2}}$
$A=24r-2{{r}^{2}}-\frac{1}{2}\pi {{r}^{2}}$
$ A'(r)=24-4r-\pi r$
$ 24-4r-\pi r=0$
$ 24=4r+\pi r$
$ 24=r(4+\pi)$
$ r=\frac{24}{4+\pi }\approx 3.36ft$
The area is maximized when the radius is $3.36$ feet and the height of the window is $3.36$ feet.
The maximum area is $40.33$ $ft^2.$
-
A lifeguard has 200 m of rope and some buoys with which she intends to enclose a rectangular area at a lake for swimming. The beach will form one side of the rectangle, with the rope forming the other three sides. Find the dimensions that will produce
the maximum area.
$A=lw$
$A(x)=x(200-2x)$
$A(x)=200x-2x^2$
$A(x)=-2x^2+200x$
$ A'(x)=-4x+200$
$ -4x+200=0$
$ -4x=-200$
$ x=50$
$ A(50)=-2{{\left( 50 \right)}^{2}}+200(50)=5000$ ${{m}^{2}}$
The maximum area possible is $5000$ $m^2.$
This can be achieved by building the swim area with the dimensions $50$ meters x $100$ meters.
-
A rancher wants to enclose two rectangular areas near a river, one for sheep and one for cattle. There is 240 meters of fencing available. If the area of the pens is to be maximized, what are their dimensions?
$A(x)=\left( \frac{240-3x}{2} \right)x$
$ A(x)=\left( 120-\frac{3}{2}x \right)x$
$ A(x)=120x-\frac{3}{2}{{x}^{2}}$
$ A'(x)=120-3x$
set $ A'=0$ to find the value of x that maximizes the area.
$ 0=120-3x$
$ 3x=120$
$ x=40$
$\text{Width=}\frac{240-3\left( 40 \right)}{2}=\frac{120}{2}=60$
The dimensions of the pens that maximize the area are 60 m x 40 m.
-
An apple farm yields an average of 30 bushels of apples per tree when 20 trees are planted on an acre of ground. Each time 1 more tree is planted per acre, the yield decreases 1 bushel per tree due to the extra congestion. How
many trees should be planted to maximize the yield?
Yield= (bushels of apples per tree) ( number of trees planted per acre)
$x$= number of trees planted ABOVE 20 trees
Yield$=(30-1x)(20+x)$
$Y(x)=600+30x-20x-{{x}^{2}}$
$Y(x)=-{{x}^{2}}+10x+600 $
$Y'(x)=-2x+10$
$-2x=-10$
$x=5$
Total trees $= 20+5=25$
Max Yield$=(30-1.5)(20+5)=625$
The yield is maximized to 625 bushels when 25 trees are planted per acre.
-
A rectangular pen is to be built with 1200 meters of fencing. The pen is to be divided into three parts using parallel partitions. Find the dimensions that will maximize the enclosed area.
$A=lw$
$ A(x)=\left( \frac{1200-4x}{2} \right)(x) $
$ A(x)=(600-2x)(x) $
$ A(x)=600x-2{{x}^{2}}$
$A'(x)=600-4x$
$0=600-4x$
$4x=600$
$x=150$
$ l=\frac{1200-4x}{2} $
$l = 600-2x$
$ l=600-2\left( 150 \right)$
$ l=600-300$
$ l=300$
The maximum area occurs when the overall dimensions of the pen are 150 m x 300 m.
-
There are 50 apple trees in an orchard, and each tree produces an average of 200 apples each year. For each additional tree planted within the orchard, the average number of apples produced drops by 5. What is the optimal number
of trees to plant in the orchard?
Yield=(number of trees)(apples produced per tree)
$ Y(t)=(50+t)(200-5t)$
$ Y(t)=10,000-250t+200t-5{{t}^{2}}$
$ Y(t)=-5{{t}^{2}}-50t+10,000$
$ Y'(t)=-10t-50$
Set $Y'(t)=0$
$ 0=-10t-50$
$ 10t=-50$
$ t=\frac{-50}{10}=-5$
Max Yield when $t=-5$
Number of trees for max yield
$50+1t$
$=50+1(-5)$
$=50-5=45$
Maximum yield
$Y(-5)=10125$
The maximum yield of $10,125$ apples occurs when $45$ trees are planted in the orchard.
-
For an outdoor concert, a ticket price of \$30 typically attracts 5000 people. For each $1 increase in the ticket price, 100 fewer people will attend.
- Find the ticket price that maximizes revenue.
Revenue = (price)(# of people)
$ R(p)=(30+1p)(5000-100p)$
$ R(p)=150,000-3000p+5000p-100{{p}^{2}}$
$ R(p)=-100{{p}^{2}}+2000p+150,000$
$ R'(p)=-200p+2000$
$ 0=-200p+2000$
$ 200p=2000$
$ p=\frac{2000}{200}=10$
Ticket price to maximize revenue $=30+1p$
$=30+1(10)$
$=40$
Maximum Revenue
$R(10)=160000$
The revenue is maximized at $\$160,000$ with a $\$40$ ticket price.
- Will your answer change if the concert area holds a maximum of 1200 people? Explain.
$p$ is defined as the number of $1.00 changes in ticket price.
$R(p)=\left( 30+1p \right)\left( 1200-100p \right)$
$ R(p)=36000-3000p+1200p-100{{p}^{2}}$
$ R(p)=36000-1800p-100{{p}^{2}}$
$ R'(p)=-1800-200p$
$ -1800-200p=0$
$ -1800=200p$
$ -9=p$
Ticket price that maximizes revenue $=30+1p$
$ =30+1\left( -9 \right)$
$ =30-9$
$ =21$
Maximum Revenue
$R(-9)=44100$
With a maximum of 1200 people, the revenue is maximized at $\$44,100$ with a ticket price of $\$21.$