MATH 1830

1.2 Finding Limits Algebraically/Infinte Limits

Pre-Class:

• Complete 1.1 Homework assignment: check and correct.
• Take notes on the videos and readings (use the space below).
• Work and check problems #1-#3b in the 1.2 NOTES section.
• Complete the 1.2 Pre-Class Quiz.

Introduction

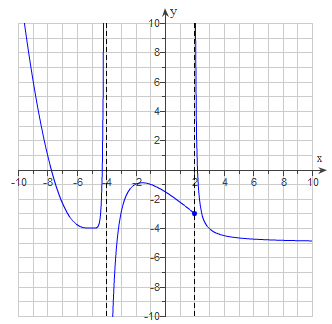
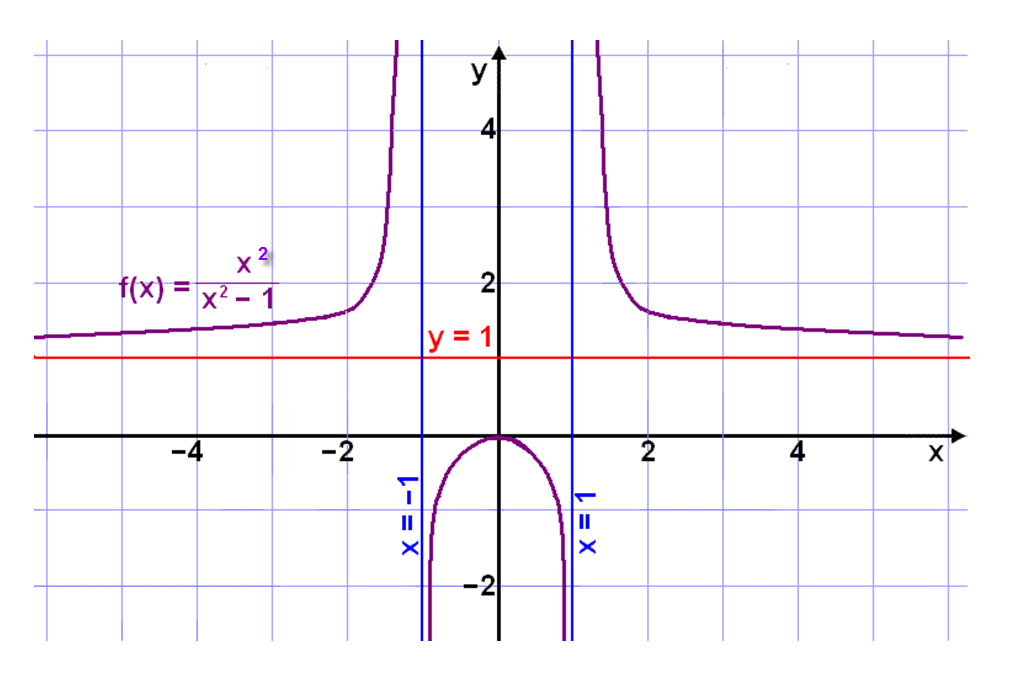
Discuss this graph with your group.

Write down everything you observe.

Be prepared to share with the class.

Notes

Find each indicated quantity, if it exists.

1. $\mathop {\lim }\limits_{x \to 4} \;{x^2} - 5x + 1 =$

   ${4^2} - 5\left( 4 \right) + 1 =$

   $- 3$

2. $\mathop {\lim }\limits_{x \to - 5} \;2{x^2} + 10x + 7 =$

   $2{\left( { - 5} \right)^2} + 10\left( { - 5} \right) + 7 =$

   $7$

3. $f\left( x \right) = \;\frac{{3{x^2}\; + 2x - 1}}{{x{\;^2} + 3x + 2}}$

   1. $\underset{x\rightarrow -3}{lim}f(x)=$

      $\underset{x\rightarrow -3}{lim}f(x)=\frac{3{{\left( -3 \right)}^{2}}~+2\left( -3 \right)-1}{\left( -3 \right){{~}^{2}}+3\left( -3 \right)+2}=\frac{20}{2}$

      $10$

   2. $\underset{x\rightarrow -1}{lim}f(x)=$

      $\frac{3{{\left( -1 \right)}^{2}}~+2\left( -1 \right)-1}{\left( -1 \right){{~}^{2}}+3\left( -1 \right)+2}=\frac{0}{0}$

      Indeterminate form. Factor, reduce, try again.

      $\underset{x\rightarrow -1}{lim}f(x)=\underset{x\rightarrow -1}{lim}\frac{\left( 3x-1 \right)\left( x+1 \right)}{\left( x+1 \right)\left( x+2 \right)}=\underset{x\rightarrow -1}{lim}\frac{\left( 3x-1 \right)}{\left( x+2 \right)}=\frac{-4}{1}$

      $-4$

   3. $\mathop {\lim }\limits_{x\; \to \;2} f\left( x \right)$ $=\frac{5}{4}=1.25$
      
   4. $\mathop {\lim }\limits_{x\; \to \; - 2} f\left( x \right)$ $=\frac{7}{0}\,$ Does not exist
      

4. $\mathop {\lim }\limits_{x \to - 5} \;\frac{{x^2\; + 7x + 10}}{{x{\;^2} + 2x -15}}$

   $=\frac{(-5)^2+7(-5)+10}{(-5)^2+2(-5)-15}=\frac{0}{0}$

   Indeterminate form. Factor, reduce, try again.

   $\underset{x\rightarrow -5}{lim}f(x)=\underset{x\rightarrow -5}{lim}\frac{\left( x+5 \right)\left( x+2 \right)}{\left( x+5 \right)\left( x-3 \right)}=\underset{x\rightarrow -5}{lim}\frac{\left( x+2 \right)}{\left( x-3 \right)}=\frac{-3}{-8}$

   $=\frac{3}{8}$

5. $\mathop {\lim }\limits_{x \to 4} \;\frac{{x^2\; -16}}{{3x{\;^2} -13x +4}}$

   $=\frac{(4)^2-16}{3(4)^2-13(4)+4}=\frac{0}{0}$

   Indeterminate form. Factor, reduce, try again.

   $\underset{x\rightarrow 4}{lim}f(x)=\underset{x\rightarrow 4}{lim}\frac{\left( x+4 \right)\left( x-4 \right)}{\left( 3x-1 \right)\left( x-4 \right)}=\underset{x\rightarrow 4}{lim}\frac{\left( x+4 \right)}{\left( 3x-1 \right)}=\frac{8}{11}$

   $=\frac{8}{11}$

6. $\underset{x\rightarrow 10}{lim} \frac{{{x^2}\; - 15x + 50}}{{{{\left( {x - 10} \right)}^2}}}$

   $=\frac{0}{0}$

   Indeterminate form. Factor, reduce, try again.

   $\underset{x\rightarrow 10}{lim}\,\frac{\left( x-5 \right)\left( x-10 \right)}{{{\left( x-10 \right)}^{2}}}=\underset{x\rightarrow 10}{lim}\,\frac{\left( x-5 \right)}{\left( x-10 \right)}=\frac{5}{0}$

   The limit does not exist. On inspection of the graph, the limit as x approaches 10 from the left and the limit as x approaches 10 from the right are not equal. There is a vertical asymptote at x=10.

7. A taxi service charges \$3.00 per mile for the first 10 miles. If the trip is over 10 miles, they charge \$5.00 per mile for every mile. Write a piecewise definition of the charge G(x) for taxi fares of x miles.

   Graph G(x) for $0 < x\; \le 25.$

   

   $f(x)= \begin{cases} 3x & 0\leq x\leq 10 \\ 5x & x > 10\\ \end{cases} $

   Find:

   $\underset{x\rightarrow10^-}{lim}G(x)=$ $30$

   $\underset{x\rightarrow10^+}{lim}G(x)=$ $50$

   $\underset{x\rightarrow10}{lim}G(x)=$ Does not exist

   

Identify the horizontal asymptotes of the following rational expression (if the horizontal asymptote exists)

8. $\underset{x\rightarrow\infty}{lim} \;\frac{{7{x^3}\; - {x^2}\; + 1}}{{5{x^3}\; + 6x\; - 7}} =$

   $\underset{x\rightarrow\infty}{lim} \;\frac{{7{x^3}\;}}{{5{x^3}\;}} = \mathop {\lim }\limits_{x \to \infty } \;\frac{{7\;}}{{5\;}} = \frac{7}{5}$

   Horizontal Asymptote at $y=\frac{7}{5}$

9. $\underset{x\rightarrow\infty}{lim} \;\frac{{6{x^4}\;-{x^2}\; + 1}}{{2{x^6}\;\; - 8x}} =$

   $\underset{x\rightarrow\infty}{lim} \;\frac{{6{x^4}\;}}{{2{x^6}}} = \underset{x\rightarrow\infty}{lim} \;\frac{{3\;}}{{{x^2}}} = 0$

   Horizontal Asymptote at $y=0$

10. $\underset{x\rightarrow\infty}{lim} \;\frac{{4{x^5}\;-\;9{x^3} - \;1}}{{5{x^3}\; + 3{x^2}\; - 7}} =$

    $\underset{x\rightarrow\infty}{lim}\;\frac{{4{x^5}\;}}{{5{x^3}\;}} = \underset{x\rightarrow\infty}{lim} \;\frac{{4{x^2}\;}}{{5\;}} = \infty $

    Because the function does not approach a specific y value as x approaches infinity, there is no horizontal asymptote.

    Vertical and Horizontal Asymptotes: A summary

    Find all vertical asymptotes, horizontal asymptotes, and holes of the function, showing all your work:

11. $f\left( x \right) = \;\frac{{2{x^2}\;\; - \;\;32}}{{{x^2}\; + \;5x\; + \;4}}$

    $f\left( x \right) = \;\frac{{2\left( {x + 4} \right)\left( {x - 4} \right)}}{{\left( {x + 4} \right)\left( {x + 1} \right)}}$

    Vertical Asymptote: x=-1

    Hole: x=-4

    Horizontal Asymptote: y=2

12. $f\left( x \right)\; = \frac{{{x^2}\;\; - \;\;9}}{{{x^2}\;\; - \;\;4}}$

    $f\left( x \right) = \;\frac{{\left( {x + 3} \right)\left( {x - 3} \right)}}{{\left( {x + 2} \right)\left( {x - 2} \right)}}$

    Vertical Asymptote: x=2 and x=-2

    Hole: none

    Horizontal Asymptote: y=1

    Find all vertical asymptotes, horizontal asymptotes, and holes of the function by a quick analysis:

13. $f\left( x \right)\; = \frac{{x\;\; + 2}}{{{x^2}\; + \;3}}$

    Vertical Asymptote: none

    Hole: none

    Horizontal Asymptote: y=0

14. $f\left( x \right)\; = \frac{{{x^2}\; - 3x - \;10}}{{{x^2}\; - \;4x - 5}}$

    $f(x) = \frac{{\left( {x - 5} \right)\left( {x + 2} \right)}}{{\left( {x - 5} \right)\left( {x + 1} \right)}}$

    Vertical Asymptote: x=-1

    Hole: x=5

    Horizontal Asymptote: y=1

15. $f(x) = \frac{{{x^2} + 5x - 14}}{{x - 2}}$

    $=\frac{(x+7)(x-2)}{x-2}$

    Vertical Asymptote: There are no vertical asymptotes.

    Hole: x=2

    Horizontal Asymptote: There are no horizontal asymptotes.